微分には非常に広く深い理論がありますが、データサイエンスにおいて重要なのは
「微分とは何を表しているのか」 を直感的に理解することです。
本記事では、
- 微分とは何か
- 接線と傾きの意味
- 導関数と増減
- 偏微分の考え方
- 勾配(勾配ベクトル)の意味
にフォーカスして解説します。
目次
1. 微分とは何をしているのか
微分を一言で表すと、
関数の各点における「変化の速さ」を調べる操作
です。
もう少し具体的には、
- 関数のある点で
- グラフに引いた 接線の傾き
を求めるのが微分です。
2. 接線と傾きのイメージ
接線とは
接線とは、ある点において曲線と「触れるように接する直線」のことです。
その点を 接点 と呼びます。


例えば、ある関数のグラフ上の点 (1, 2) において引かれた直線が接線です。
この接線の 傾き が、その点での微分値になります。
3. 導関数とは
関数を
f(x)
としたとき、その微分を
f′(x)
と書き、これを 導関数 と呼びます。
導関数は、
「x の値を与えると、その点での接線の傾きを返す関数」
です。
例:2次関数の場合
たとえば、
f(x) = x²
とすると、その導関数は
f′(x) = 2x
になります。
- x = 1 のとき → 傾きは 2
- x = 0 のとき → 傾きは 0
つまり、導関数を使うことで「どの点でどれくらい傾いているか」が分かります。
4. dx という表記の意味
微分の厳密な定義では、「ある一点の周りを非常に細かく見る」ことを考えます。
そのため、
- Δx(変化量)
の代わりに - dx(極めて小さい変化)
という記号を使うことがあります。
dx は「限りなく小さい変化」を表す記号だと理解しておけば十分です。
5. 1次関数の微分
f(x) が 1次関数(直線)の場合、
- 接線は元の直線そのもの
- 傾きはどこでも一定
になります。
そのため、導関数は 定数関数 となり、その値は直線の傾きに一致します。
6. 導関数と関数の増減
導関数の 符号(プラスかマイナスか) に注目すると、関数の振る舞いが分かります。
- f′(x) > 0 :関数は増加
- f′(x) < 0 :関数は減少
極大点・極小点
f′(x) = 0 となる点では、
- 増加 → 減少 に変わる
- 減少 → 増加 に変わる
ことがあります。
このような点を、
- 極大点
- 極小点
と呼びます。
ただし、微分が 0 だから必ず極値とは限らない ことに注意が必要です。
7. 2階の導関数
極大点か極小点かを判断するために使うのが、
導関数をさらに微分したもの
で、これを 2階の導関数 と呼びます。
- 2階導関数が正 → 極小
- 2階導関数が負 → 極大
といった判定に利用されます。
8. 変数が複数ある場合の問題
ここまでは、変数が1つの関数
f(x)
を扱ってきました。
しかし、ビジネスやデータ分析では、
- 売上 × 広告費 × 時期
- 価格 × 評価 × 在庫
など、複数の変数が同時に関係する関数 を扱うのが普通です。
例えば、
f(x, y)
のような関数を考えます。
9. 偏微分とは何か
2変数関数 f(x, y) において、
- y を定数とみなして
- x だけを変化させたときの微分
を 偏微分 といいます。
偏導関数の表記
- x で偏微分したもの
∂f / ∂x
- y で偏微分したもの
∂f / ∂y
と表します。
これは、
「他の変数は固定したまま、1つの変数だけの影響を見る」
という考え方です。
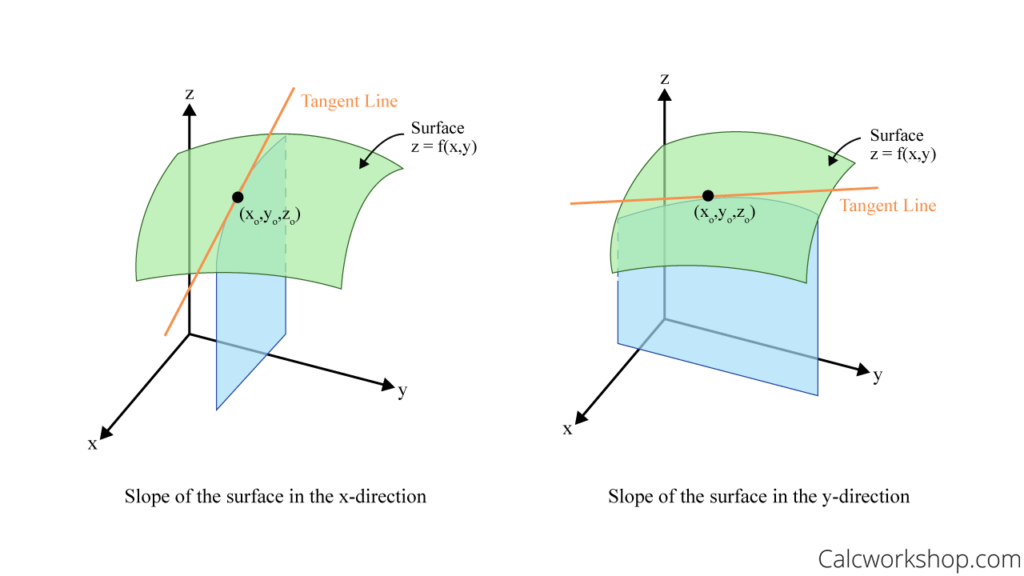
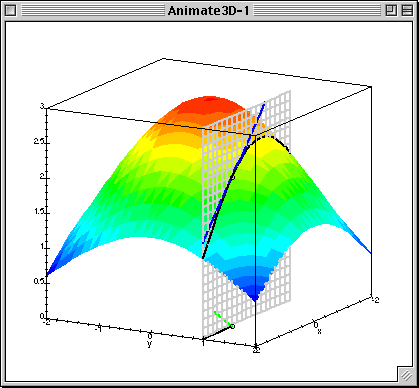
10. 偏微分をさらに行う
偏導関数をさらに偏微分することも可能です。
- ∂²f / ∂x²
- ∂²f / ∂x∂y
といった形で表されます。
2変数関数の極大・極小の判定では、これらが重要な役割を果たします。
11. 勾配(勾配ベクトル)とは
偏微分の最も重要な応用が 勾配(gradient) です。
n 変数の関数
f(x₁, x₂, …, xₙ)
について、
- 各変数で偏微分した値を並べたもの
が 勾配ベクトル です。
勾配の意味
勾配には次の重要な意味があります。
① 勾配の向き
→ 関数 f の値が 最も大きく増加する方向
② 勾配の大きさ
→ その方向に十分小さい距離 C 進むと、
関数の値は 勾配 × C 程度 増加する
この性質は、機械学習の 勾配降下法 の理論的基盤になります。
12. 学習ポイント(重要)
● 偏微分とは何かを理解する
● 意味を意識して計算できるようになる
微分・偏微分・勾配は、数式として覚えるだけでなく、
「何がどれくらい変わるのかを見ている操作」
だと理解することが、データサイエンスでは何より重要です。
まとめ
- 微分は「接線の傾き」を求める操作
- 導関数は「傾きを返す関数」
- 符号を見ると増減が分かる
- 偏微分は「他を固定して1変数を見る」考え方
- 勾配は「最も増加する方向」を示す
これらはすべて、
最適化・機械学習・統計モデルの基礎につながる重要概念です。
【2026年1月版】データサイエンティスト検定 おすすめ参考書・問題集ランキング
データサイエンティスト検定は、データサイエンティストに必要なスキルを問う資格として人気が高まっています。 学生から社会人まで幅広い受験者がいて、「どの参考書を選べばいいか迷う」という声も多く聞かれます。
この記事では、各級ごとにおすすめの参考書・問題集をランキング形式でご紹介します。 2026年版として最新の情報にアップデートしていますので、これから勉強を始める方はぜひ参考にしてください。
👤 本記事の執筆者について

運営者:トモタツ
・広告代理店でのデータ運用経験を経て、IT企業でデータサイエンティストとして活躍。
・大手企業のデータサイエンスチームリーダーとして、ビジネス戦略に統計分析を活用。
・機械学習モデルの設計から運用までを担当し、プロジェクトマネージャーとしても多数の案件を成功に導く。
実務での統計活用経験をもとに「分かりやすく・使える統計」を意識して記事を執筆しています。
🔍 選書の基準
本記事で紹介する参考書は、以下の観点から選定しています:
- 実際に使ってみて学習効果が高かったか
- 独学者でも使いやすい構成かどうか
- 試験対策としての網羅性・実践力の有無
- 読者のレベル別(初心者〜中級者)に合わせやすいか
特に「必須レベル(重要度)」「難易度」「理解のしやすさ/実践力アップ/理論の深さ」といった軸で評価し、学習目的に合った書籍を選びやすくしています。
📘 データサイエンティスト検定 おすすめ参考書ランキング【2026年版】
🥇 第1位:最短突破 データサイエンティスト検定(リテラシーレベル)公式リファレンスブック 第3版

📖データサイエンティストに必要なスキルを本質的に理解したい人に最適な学術的な教科書です。
💴 価格:2,860 円(税込)
⭐ 必須レベル:★★★★★
⭐ 難易度:★★★★☆
⭐ 実践力アップ:★★★☆☆
✅ 本番と似た形式のテスト付属
✅ 解説が詳細で学習のペースをつかみやすい
✅ 独学でも十分に対応可能
🥈 第2位:徹底攻略データサイエンティスト検定問題集[リテラシーレベル]対応 第2版

📖 過去問を収録した公式の問題集で、実際の試験形式や出題傾向に最も忠実です。
💴 価格:2,750 円(税込)
⭐ 必須レベル:★★★★☆
⭐ 難易度:★★★★☆
⭐ 実践力アップ:★★★★★
✅ 本番と同じ出題形式
✅ 解説が詳細で学習のペースをつかみやすい
✅ 独学でも十分に対応可能
🥉 第3位:データサイエンティスト検定[リテラシーレベル][徹底解説+良質問題+模試(PDF)] 最強の合格テキスト

📖合格に向けて必要な知識と出題傾向を網羅しているテキスト。
💴 価格:3,861 円(税込)
⭐ 必須レベル:★★★☆☆
⭐ 難易度:★★★★★
⭐ 実践力アップ:★★★★☆
✅ 出題形式そのまま
✅ 解説がわかりやすい
✅ 本番前の力試しにも最適
✅ まとめ
📊 データサイエンティスト検定 参考書比較表(まとめ)
| 書籍名 | 金額(税込) | 必須レベル | 難易度 | 特徴 | 購入リンク |
|---|---|---|---|---|---|
| 最短突破 データサイエンティスト検定 | 2,860 円 | ★★★★★ | ★★★★☆ | 中級者向け、丁寧な解説、図解豊富 | Amazon |
| 徹底攻略データサイエンティスト検定問題集 | 2,750 円 | ★★★★☆ | ★★★★☆ | 本番形式、過去問収録、実践向き | Amazon |
| データサイエンティスト検定[リテラシーレベル][徹底解説+良質問題+模試(PDF)] | 3,861 円 | ★★★☆☆ | ★★★★☆ | 問題集、解説付き | Amazon |
まずは「過去問ベース」+「解説が丁寧な参考書」を1冊ずつ揃えることをおすすめします。
効率よく学習して、データサイエンティスト検定合格をつかみましょう!


