データサイエンスでは、「条件に合うデータの集まり」を扱う場面が頻繁にあります。
その基礎となるのが 集合 と 集合演算 の考え方です。
本記事では、
- 和集合・積集合・差集合などの基本演算
- ベン図による直感的理解
- Pythonでの書き方
- 集合演算と論理演算の対応関係
について解説します。
目次
1. 和集合(Union)
定義
和集合とは、
2つの集合のうち、少なくともどちらか一方に含まれる要素 の集合です。
演算記号では
- A ∪ B
と表します。


ベン図では、A と B の 両方を含む全体 が和集合にあたります。
Pythonでの表記
Python では、集合(set)に対して次の演算子を使います。
A | B
2. 積集合(Intersection)
定義
積集合とは、
2つの集合の両方に共通して含まれる要素 の集合です。
演算記号では
- A ∩ B
と表します。
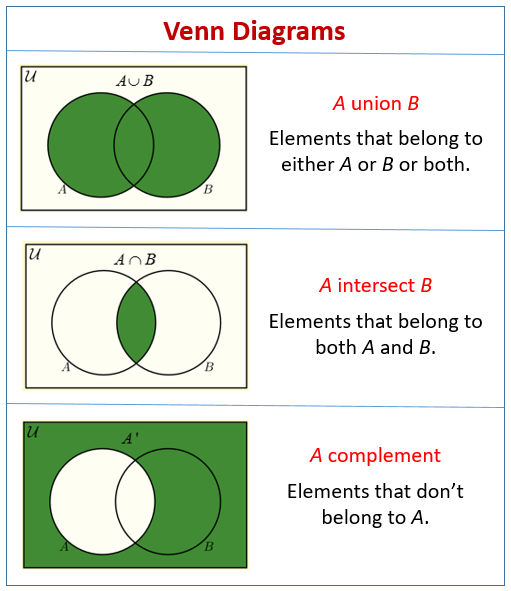
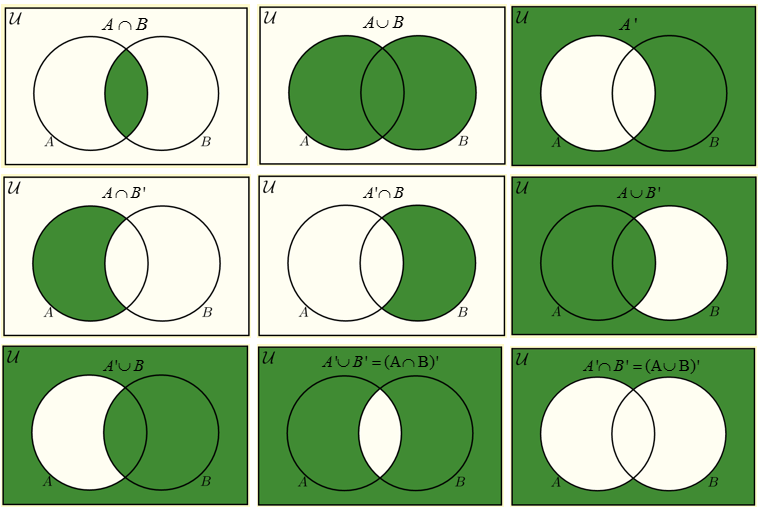
ベン図では、A と B が 重なっている部分 が積集合です。
Pythonでの表記
A & B
3. 差集合(Difference)
定義
差集合とは、
ある集合から、もう一方の集合に含まれる要素を除いた集合 です。
演算記号では
- A − B
と表します。
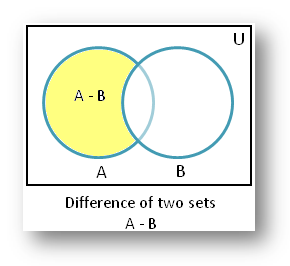

これは、
- A には含まれる
- B には含まれない
要素の集合を意味します。
Pythonでの表記
A - B
4. 対称差集合(Symmetric Difference)
定義
対称差集合とは、
2つの集合のうち、どちらか一方にのみ含まれる要素 の集合です。
演算記号では
- A △ B
と表します。
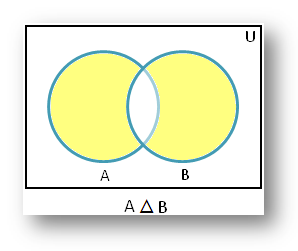

ベン図では、A と B の 重なっていない部分だけ が該当します。
Pythonでの表記
A ^ B
5. 補集合(Complement)
定義
補集合とは、
ある集合に含まれない要素の集合 です。
演算記号では
- Aᶜ
- または Ā
のように表されます。
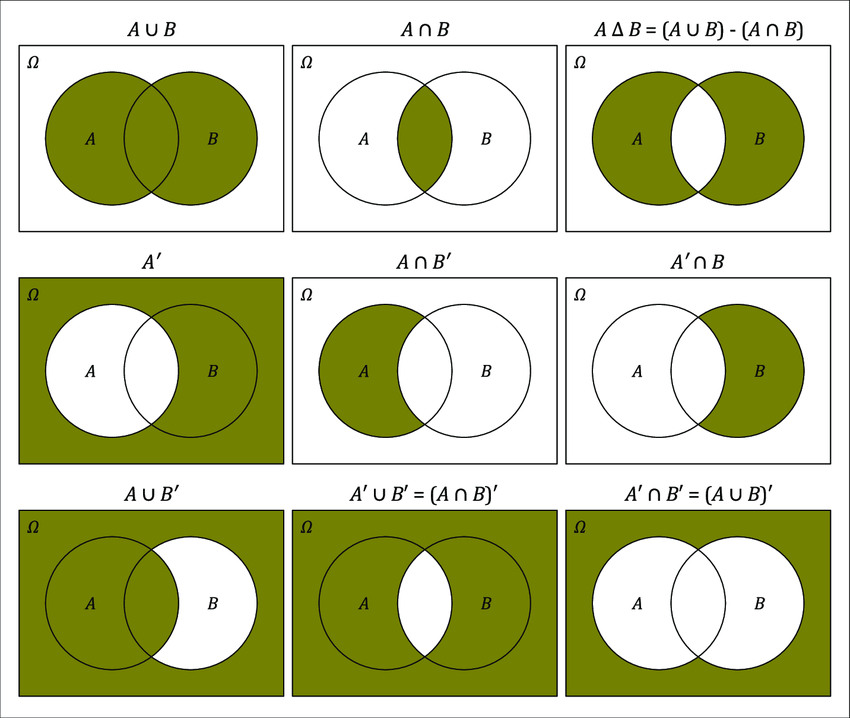
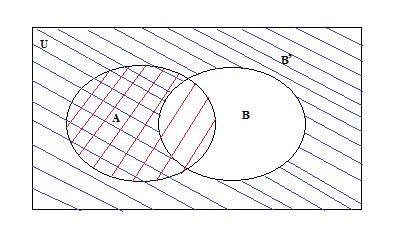
全体集合が必要な理由
補集合を定義するには、
どこまでが全体なのか(全体集合)
を明確に決める必要があります。
そのため、
- 「単純にAの補集合を求める」
という操作は定義できず、
Pythonなどのプログラミング言語でも 補集合専用の演算子は用意されていません。
実装する場合は、
U - A
のように、全体集合 U を明示する必要があります。
6. 集合演算とは何か
集合演算とは、
- 要素の集合に対して
- 和・積・差などの操作を行うこと
を指します。
データ分析では、
- 条件に合うデータの抽出
- 複数条件の組み合わせ
- フィルタリング
といった場面で頻繁に使われます。
7. 集合演算と論理演算の違い
一方で、論理演算 は、
- 真(True)
- 偽(False)
の2通りの値を取る 真偽値 に対する演算です。
集合演算と論理演算は、次のように対応しています。
集合演算と論理演算の対応表
| 集合演算 | 記号 | 論理演算 | 意味 |
|---|---|---|---|
| 和集合 | A ∪ B | OR | どちらかが真 |
| 積集合 | A ∩ B | AND | 両方が真 |
| 差集合 | A − B | AND NOT | AかつBでない |
| 対称差集合 | A △ B | XOR | どちらか一方のみ真 |
| 補集合 | Aᶜ | NOT | 真偽の反転 |
この対応を理解すると、
- 集合の話
- 条件分岐(if文)
- データ抽出条件
を統一的に理解できるようになります。
まとめ
- 和集合:どちらかに含まれる要素
- 積集合:両方に含まれる要素
- 差集合:一方から他方を除く
- 対称差集合:片方だけに含まれる
- 補集合:全体集合からの除外
- 集合演算と論理演算は強く対応している
集合演算は、
統計・データ分析・プログラミングの共通言語 と言える重要な基礎概念です。


