相関係数を勉強していると、必ず出てくるのが
- ピアソンの積率相関係数
- スピアマンの順位相関係数
という2つの指標です。
教科書では
「ピアソンは線形」「スピアマンは順位」
と書かれていますが、それだけでは正直わかりにくい。
そこでこの記事では、
具体的なデータ例を使いながら
この2つの違いを説明します。
目次
1. 相関係数とは「一緒に動いているか」を見る指標
まず前提として、相関係数は
2つの数値が、同じ方向に動いているかどうか
を表します。
具体例①:勉強時間とテスト得点
| 勉強時間(時間) | 得点 |
|---|---|
| 1 | 40 |
| 2 | 50 |
| 3 | 60 |
| 4 | 70 |
| 5 | 80 |
勉強時間が増えると、得点も増えています。
このような関係を
「相関がありそう」と感じるのは自然です。
2. ピアソンの積率相関係数を具体例で見る
ピアソン相関が得意な例(直線的な関係)
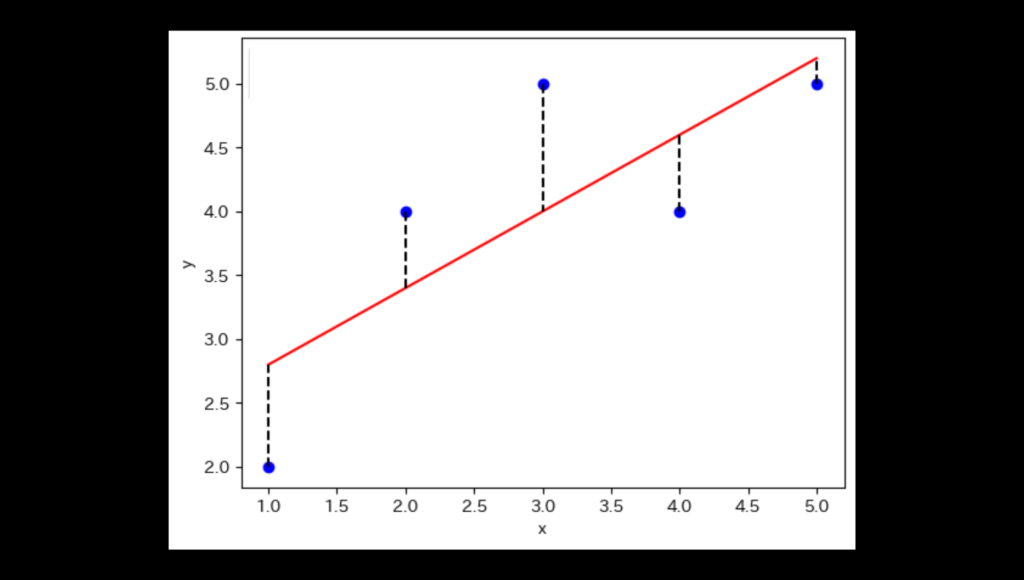
上の「勉強時間と得点」の例を散布図にすると、
点はほぼ一直線に並びます。
このような場合、
- 勉強時間が1時間増える
- 得点もだいたい同じだけ増える
という 直線的な関係 があります。
👉 このときに使うのが
ピアソンの積率相関係数です。
ピアソン相関は、
「この直線関係はどれくらいきれいか?」
を数値で表しています。
ピアソン相関がうまくいかない例
次のデータを見てください。
具体例②:学習時間と理解度(曲線的)
| 勉強時間 | 理解度 |
|---|---|
| 1 | 20 |
| 2 | 35 |
| 3 | 55 |
| 4 | 80 |
| 5 | 95 |
最初はゆっくり伸び、
途中から一気に理解度が上がっています。
散布図にすると、
カーブを描く形になります。
この場合、
- 明らかに関係はある
- でも直線ではない
ため、
ピアソン相関は思ったより低い値になることがあります。
3. スピアマンの順位相関係数を具体例で見る
スピアマン相関の考え方
スピアマン相関では、
数値をそのまま使いません。
代わりに、順位に変換します。
具体例③:順位に直してみる
先ほどの「学習時間と理解度」を
順位で書き直します。
| 勉強時間 | 理解度 | 勉強時間の順位 | 理解度の順位 |
|---|---|---|---|
| 1 | 20 | 1 | 1 |
| 2 | 35 | 2 | 2 |
| 3 | 55 | 3 | 3 |
| 4 | 80 | 4 | 4 |
| 5 | 95 | 5 | 5 |
順位を見ると、
- 勉強時間が長い人ほど
- 理解度の順位も高い
という関係は完全に一致しています。
👉 このようなとき、
スピアマンの順位相関係数は高くなります。
4. 外れ値があるときの違い(重要な例)
具体例④:外れ値が混じるケース
| 勉強時間 | 得点 |
|---|---|
| 1 | 40 |
| 2 | 50 |
| 3 | 60 |
| 4 | 70 |
| 5 | 150 |
最後の1人だけ、極端に高得点です。
ピアソン相関の場合
- 数値の大きさを使う
- 150点が強く影響する
→ 相関係数が大きく歪みます。
スピアマン相関の場合
順位にすると:
| 勉強時間順位 | 得点順位 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
外れ値でも
順位は「1つ上がるだけ」。
👉 そのため、
スピアマン相関は外れ値の影響を受けにくい。
5. ピアソンとスピアマンの違いを整理
| 観点 | ピアソン | スピアマン |
|---|---|---|
| 使う値 | 数値そのもの | 順位 |
| 得意な関係 | 直線的 | 増え続ける/減り続ける |
| 曲線的関係 | 苦手 | 得意 |
| 外れ値 | 影響大 | 影響小 |
6. どちらを使えばいいか(具体例ベース)
- 勉強時間と得点がほぼ直線的
→ ピアソン相関 - 努力量と成長度合い(途中で伸びが変わる)
→ スピアマン相関 - 順位・ランキング・評価点
→ スピアマン相関
7. まとめ(初心者向け結論)
- ピアソン相関は「直線のきれいさ」を見る
- スピアマン相関は「順番が合っているか」を見る
- 同じデータでも、結果が変わることがある
- 大切なのは「何を知りたいか」
相関係数は、
公式よりも具体例で理解するほうが早い指標です。
ここまでの例を思い出せれば、
ピアソンとスピアマンで迷うことはほぼなくなります。