統計学や確率の分野では、「組み合わせ」を計算する場面が多く出てきます。その際によく使われるのが「C」を使った表記法です。この記事では、組み合わせの基礎から「C」の具体的な計算方法、応用例までを詳しく解説します!
そもそも組み合わせとは?
組み合わせとは、特定のグループからいくつかの要素を選ぶ方法の総数を指します。
特徴:
- 順序を考慮しない
- グループ内の選び方だけに注目
例:
クラスに5人の生徒(A, B, C, D, E)がいる場合、3人を選ぶ方法は以下の通り:
- {A, B, C}, {A, B, D}, {A, B, E}, {A, C, D}, {A, C, E}, {A, D, E}…
これらを計算するのが「C」を使った組み合わせ計算です。
組み合わせの公式
組み合わせを計算する公式は次のようになります:
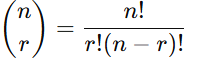
- n: 全体の要素数
- r: 選ぶ要素数
- n!: n の階乗(n×(n−1)×(n−2)×…×1)
この式は「n個の中からr個を選ぶ場合の数」を表します。
具体例で理解する
例題1: 5人の生徒から3人を選ぶ場合
ここでは、組み合わせを求める公式に当てはめます。
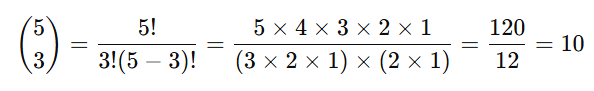
答えは 10通り です。
例題2: 10枚のカードから2枚を選ぶ場合
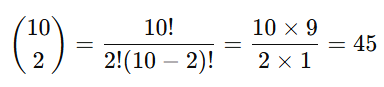
組み合わせの「C」の使い方
数学の式やプログラム内では、以下のように表記されます:
- 数学表記:
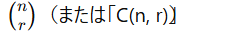
- 計算機表記
nCr(電卓やプログラミング言語で用いる場合)
Excelで計算する場合: Excelの組み合わせ計算には COMBIN 関数を使用します。
例:=COMBIN(10, 2) と入力すると、10個の中から2個を選ぶ場合の組み合わせ数(45)が計算されます。
組み合わせの応用例
1. 抽選や宝くじ
- 宝くじで6個の数字を選ぶ場合、43個から6個を選ぶ方法は:
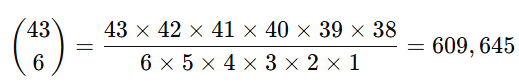
つまり、60万通り以上の可能性があります。
2. サンプル調査
例えば、1000人の中からランダムに50人を選びたい場合も、組み合わせで計算します。ただし、通常は全通りを数えるのではなく、適切なサンプル抽出法を使用します。
3. ポーカーの役の計算
ポーカーでは、52枚のカードから5枚を選ぶ組み合わせが考えられます。
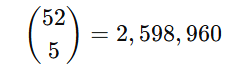
これを元に役の確率を求めることが可能です。
まとめ
「C」を使った組み合わせの計算は、統計学や確率論で頻出する重要な手法です。この計算を使えば、実際の問題に応じた正確な数値を得ることができます。
ポイント:
- 組み合わせは「順序を考えない」選び方を求める方法。
- 計算公式 nCr は必ず覚えておきましょう!