世の中の多くの不確実な現象は、確率分布 を用いて表現できます。
確率分布を理解することで、「どの事象がどの程度の頻度で起こるのか」を定量的に扱えるようになります。
確率分布は、大きく次の2種類に分類されます。
- 離散型確率分布
- 連続型確率分布
本記事では、それぞれの代表的な分布と、その意味・使いどころを解説します。
目次
1. 確率分布とは何か
確率分布とは、
確率変数が、どの値をどの確率で取るのかを表したもの
です。
確率変数が取りうる値の性質により、
- 自然数など 飛び飛びの値 → 離散型確率分布
- 実数全体のような 連続した値 → 連続型確率分布
に分かれます。
2. 離散型確率分布
定義
離散型確率分布とは、
確率変数が有限個、または無限個であっても
自然数と対応づけられるような離散的な値のみを取る場合の確率分布
です。
例:
- サイコロの目
- 1日のメールの件数
- コインの表が出た回数
2.1 ベルヌーイ分布
概要
ベルヌーイ分布は、
結果が2通りしかない試行の結果を
0 と 1 で表した確率分布
です。
例:
- 成功 / 失敗
- 表 / 裏
このような試行を ベルヌーイ試行 と呼びます。
利用例
- コインの表が出る確率
- メールを開封したかどうか(開封=1、未開封=0)
2.2 二項分布
概要
二項分布とは、
互いに独立なベルヌーイ試行を n 回行ったときに
注目する事象が x 回起こる確率
を表す確率分布です。
具体例
- コインを n 回投げたときに表が x 回出る確率
- 広告を n 回表示したときにクリックが x 回起こる確率
二項分布は、「回数」を扱う非常に汎用的な分布 です。
2.3 ポアソン分布
概要
ポアソン分布とは、
単位時間あたり平均 λ 回起こる現象が
ある時間内に x 回起こる確率
を表す確率分布です。
特徴と例
- 稀な現象を表現するのに適している
- 発生回数に上限がない
例:
- 1日平均1件の交通事故が起こる地域で、3日間事故が起こらない確率
- サーバー障害の発生回数
3. 連続型確率分布
定義
連続型確率分布とは、
確率変数が実数値を取る場合の確率分布
です。
例:
- 身長
- 体重
- 待ち時間
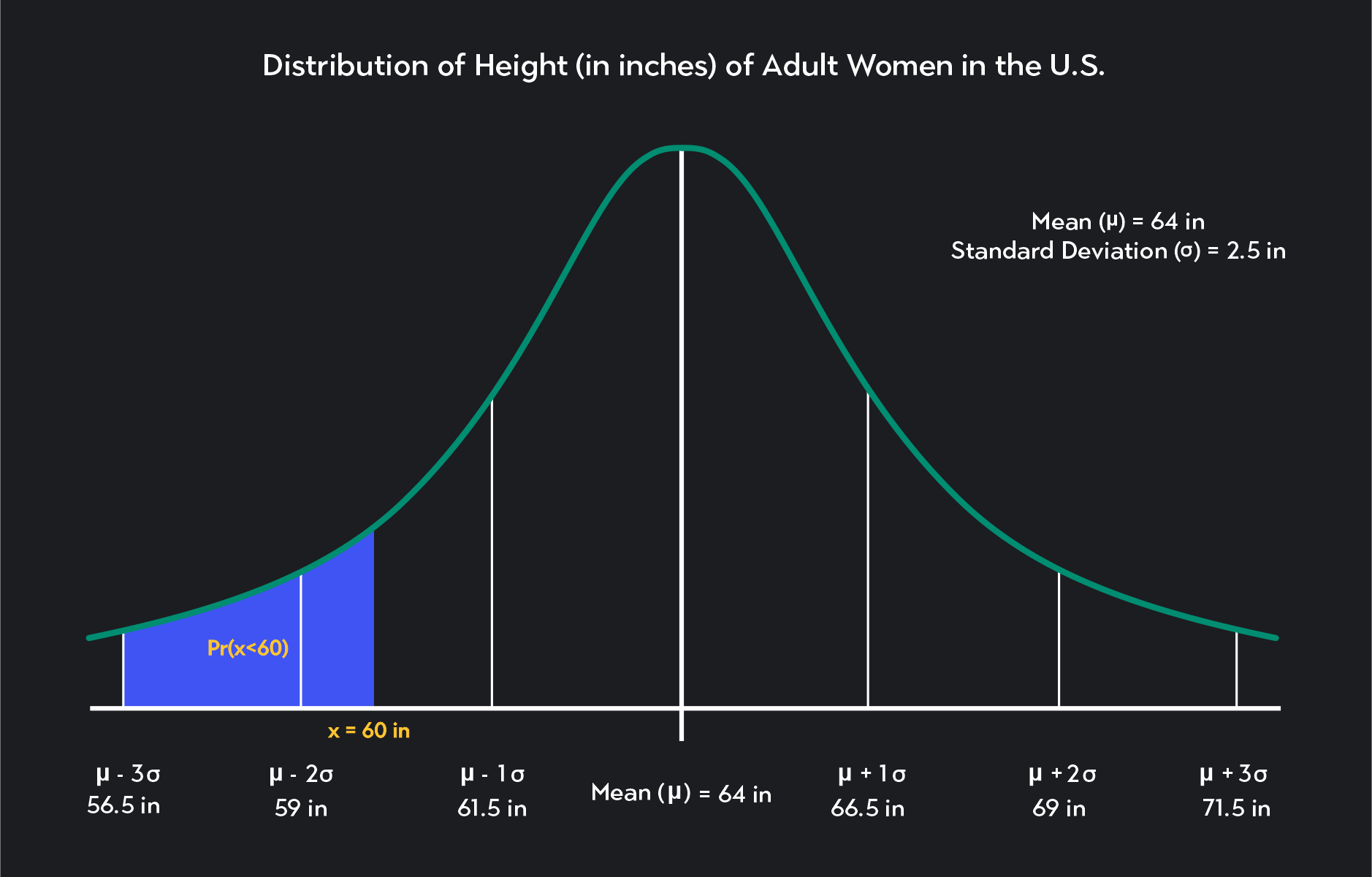
3.1 正規分布
概要
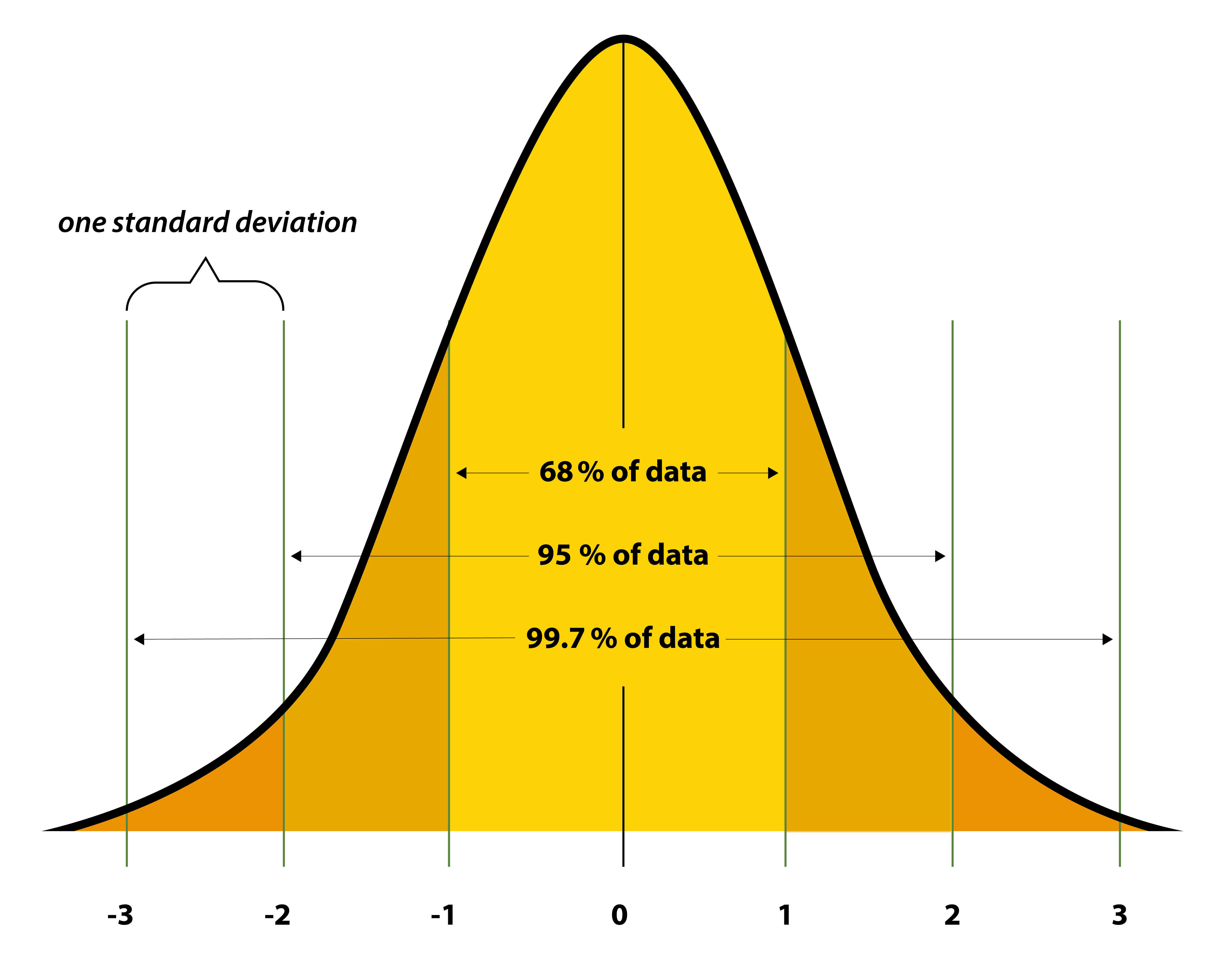
正規分布とは、
平均・中央値・最頻値が一致し、
平均を中心に左右対称な連続型確率分布
です。
理論的に扱いやすく、統計学の中心的存在です。
利用例
- 身長が180cm以上の人の割合
- 試験の点数分布
- 標本数が大きい場合の標本平均の分布
3.2 指数分布
概要
指数分布とは、
単位時間あたり平均 λ 回起こる現象について、
次に起こるまでの時間が x である確率
を表す連続型確率分布です。
具体例
- 1時間に平均10人来店する店で、10分以内に次の客が来る確率
- サーバーに次のアクセスが来るまでの待ち時間
3.3 カイ二乗分布
概要
カイ二乗分布とは、
互いに独立な標準正規分布に従う確率変数の二乗和が従う分布
です。
利用シーン
- 誤差の二乗和
- 統計的検定(カイ二乗検定など)
実務では「検定でよく出てくる分布」として押さえておくことが重要です。
4. 二項分布と正規分布の関係
二項分布は、
- ベルヌーイ試行の回数 n を増やす
ことで、正規分布に近づく ことが知られています。
イメージ
- n = 10 → 分布はギザギザ
- n = 20, 50, 100 → なめらかな形に近づく
試行回数を無限に増やすと、
二項分布は 正規分布で近似可能 になります。
正規近似の利点
二項分布の確率計算には、
- 組み合わせ
- 累乗
が含まれるため、n が大きくなると計算量が急増します。
一方で、
二項分布を正規分布で近似することで
計算コストを大幅に削減できる
という利点があります。
さらに、標準化を行えば
標準正規分布 として扱うことも可能です。
まとめ
- 確率分布は「事象の起こりやすさ」を表す枠組み
- 離散型:ベルヌーイ分布・二項分布・ポアソン分布
- 連続型:正規分布・指数分布・カイ二乗分布
- 二項分布は試行回数が大きいと正規分布で近似可能
- 正規近似は計算コスト削減に有効
確率分布の理解は、
統計的推定・検定・機械学習モデルの前提
となる極めて重要な基礎です。


