目次
1. はじめに（標準偏差とは何か？）
統計学を学ぶと必ず登場する「標準偏差」。
データのばらつきを表す指標ですが、数式を見て苦手意識を持つ人も多いかもしれません。
しかし、標準偏差はデータ分析や統計的な意思決定に欠かせない重要な指標です。
例えば、以下のような場面で使われます。
- テストの成績（成績のバラつきを知る）
- 投資のリスク分析（株価の変動幅を測る）
- 製品の品質管理（製品のばらつきを管理する）
本記事では、標準偏差の計算方法や使い方を初心者向けにわかりやすく解説します！
2. 標準偏差の定義と計算方法
2.1 標準偏差とは？
標準偏差（Standard Deviation, SD）とは、データが平均値からどれくらい散らばっているかを示す指標です。
記号として「σシグマ）」または「sss」が使われます。
直感的に理解すると：
- 標準偏差が小さい → データのばらつきが少ない
- 標準偏差が大きい → データのばらつきが大きい
2.2 標準偏差の計算方法
標準偏差は以下の手順で計算されます。
母集団の標準偏差（σ）
母集団（全体のデータ）の標準偏差は次の式で求められます。
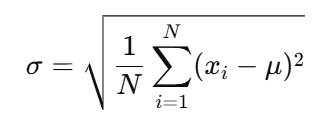
- xi ：各データの値
- μ ：平均値（データの中心）
- N ：データの総数
標本の標準偏差（s）
標本（母集団の一部を抜き出したデータ）の標準偏差は次の式で求められます。
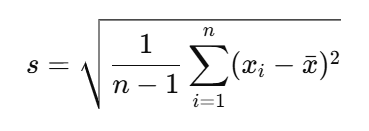
- xˉ ：標本平均（標本データの中心）
- n ：標本のデータ数
- 「n−1」とすることで、不偏推定量として母集団をより正確に推測できる
3. 分散との違いとは？
標準偏差とよく混同される指標に「分散（Variance）」があります。
3.1 分散とは？
分散は、標準偏差を求める途中で出てくる数値であり、データのばらつきを二乗したものです。
分散の公式は以下の通りです。
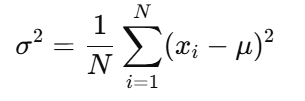
標準偏差は、この分散の平方根をとったものです。
3.2 なぜ標準偏差を使うのか？
- 分散は「平方」されているため、元の単位と異なる値になってしまう
- 標準偏差なら元のデータと同じ単位で解釈できる
例えば：
- テストの点数が 50点・60点・70点 なら、分散は「点の2乗」になるが、標準偏差は「点」のまま
4. 標準偏差が大きいとどうなる？小さいとどうなる？
4.1 標準偏差が小さい場合
データのばらつきが小さく、平均値に集まっていることを意味します。
例：
| 数値データ | 平均値 |
|---|---|
| 48 | 50 |
| 50 | 50 |
| 52 | 50 |
このようにデータが50付近に集中している場合、標準偏差は小さくなります。
4.2 標準偏差が大きい場合
データのばらつきが大きく、平均値から離れた値が多いことを意味します。
例：
| 数値データ | 平均値 |
|---|---|
| 30 | 50 |
| 50 | 50 |
| 70 | 50 |
この場合、データのバラつきが大きく、標準偏差も大きくなります。
5. 実際のデータを使った標準偏差の計算（Pythonコード付き）
Python を使って、標準偏差を求めてみましょう！
import numpy as np
# データセット
data = [48, 50, 52, 30, 50, 70]
# 母集団の標準偏差
std_population = np.std(data)
print(f"母集団の標準偏差: {std_population}")
# 標本の標準偏差
std_sample = np.std(data, ddof=1)
print(f"標本の標準偏差: {std_sample}")
出力結果
編集する母集団の標準偏差: 12.041
標本の標準偏差: 13.856
このように、標準偏差の計算は Python を使うと簡単にできます！
6. 標準偏差の応用例
標準偏差は、さまざまな分野で使われています。
6.1 ビジネスでの活用
- 売上の変動を分析し、安定した成長をしているかを判断
- 商品の不良率のばらつきを測定し、品質管理に活用
6.2 投資・金融
- 株価の変動幅を測定し、リスクの高い銘柄を特定
- 投資ポートフォリオのリスク管理に活用
6.3 教育
- テストの成績のばらつきを分析し、試験の難易度を評価
- 学力差が大きい場合、個別指導の必要性を判断
7. まとめ
- 標準偏差はデータのばらつきを表す指標
- 分散の平方根をとることで、元の単位と同じ尺度で比較可能
- 標準偏差が小さい → データが平均値に集中
- 標準偏差が大きい → データがばらついている
- Pythonを使うと簡単に計算できる！
標準偏差を理解することで、データの特徴を正しく捉え、適切な分析ができるようになります！
