正規分布は、データ分析や統計学で最も重要な分布の一つで、多くの自然現象や人間の特性がこの分布に従うことが多いとされています。この記事では、正規分布の特徴とその応用方法について詳しく解説します。
正規分布とは?
正規分布とは、平均値を中心に左右対称な形をした分布で、鐘のような形をしていることから「ベル曲線」とも呼ばれます。この分布は「平均を中心にデータが集まりやすい」「左右対称」「極端な値は少ない」という特徴を持ちます。
正規分布の例
- 人間の身長や体重
- 試験の点数
- 製品の寸法誤差
- 調査対象の多くが平均に集まるような自然現象
正規分布の3つの主要な特徴
正規分布には3つの主要な特徴があり、これらを理解することで、データが正規分布に従っているかどうかの判断がつきやすくなります。
1. 平均、中央値、最頻値が一致する
正規分布では、平均値、中央値、最頻値が同じ値を取ります。このため、左右対称でバランスの取れた形になります。
2. 分布が左右対称
正規分布の形は、平均値を中心に左右対称です。つまり、平均値からのズレが同じであれば、左右どちらに離れても発生頻度が同じです。
3. 中央からの離れ具合を表す「68-95-99.7ルール」
正規分布では、データの約68%が平均値から±1標準偏差の範囲に、約95%が±2標準偏差の範囲に、そして約99.7%が±3標準偏差の範囲に収まるという法則があります。この特性を活用して、異常値や外れ値の検出に役立てられます。
正規分布の数式とグラフの特徴
正規分布は以下の確率密度関数で表されます。
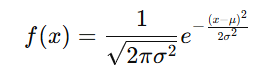
ここで、
- μは平均
- σは標準偏差
グラフの特徴
- 幅広く緩やか:標準偏差が大きいほど広がり、データのばらつきが大きいことを示します。
- 鋭く高い:標準偏差が小さいほど狭く高い形になり、データが平均値に集中していることを表します。
正規分布の応用例
正規分布は、統計的手法の多くで基本的な前提条件となっており、ビジネスや研究などさまざまな分野で応用されています。
1. 品質管理
製品の寸法や重さなどが正規分布に従う場合、ある範囲内に収まるかどうかを確認することで、不良品の割合を推測できます。この手法は「管理図」として利用され、製品の品質を一定に保つために役立ちます。
2. 異常検知
金融や製造業では、正規分布から外れる異常値を検出するために利用されます。異常値を発見することで、製品の不具合や不正な取引を早期に発見できる可能性が高まります。
3. 生物学的データの分析
身長や体重、血圧など、生物学的データはしばしば正規分布に従うとされています。正規分布の特徴を利用することで、集団の健康状態や平均的な数値を分析するのに役立ちます。
4. 試験のスコア分析
多くのテストや試験の得点は正規分布に従います。正規分布を仮定することで、平均点や偏差値、得点のばらつき具合を分析し、標準偏差を利用して成績の評価基準を設けることが可能です。
5. 株価やリスク管理
株価や利回りも正規分布に従うと仮定されることが多く、特に金融工学の分野ではリスク評価やポートフォリオ管理に正規分布が応用されます。
データが正規分布に従うか確認する方法
1. ヒストグラムでの確認
ヒストグラムは、データの分布を視覚的に把握するためのツールです。正規分布に従うデータの場合、ヒストグラムは「鐘の形」に近い左右対称の形状を示します。以下がポイントです:
- 左右対称であるか:正規分布は平均値を中心に左右対称な形をしています。
- 尖度や歪度が適度か:尖度が高すぎると尖った形、低すぎると平坦な形になり、正規分布とは異なる可能性があります。歪度がある場合も正規分布からの逸脱が疑われます。
ヒストグラムで大まかな形状を確認することで、正規分布に近いかどうかを視覚的に判断できますが、あくまで「おおよその形状」をつかむのに向いており、厳密な確認には次に紹介する統計的な手法が効果的です。
2. Q-Qプロット(Quantile-Quantile Plot)
Q-Qプロットは、データの分布と理論上の正規分布との関係を可視化する方法です。以下のステップで確認できます:
- データの順序付け:観測データを小さい順に並べておきます。
- 理論分布との比較:観測データと、正規分布に従う場合の同じ位置にある理論的な分位点とを比較します。
- 直線に乗るか確認:Q-Qプロット上でデータが直線的に並んでいれば、そのデータは正規分布に従っている可能性が高いと判断できます。
Q-Qプロットの解釈
- 直線に沿う場合:データが正規分布に従っていると考えられます。
- 直線から離れる場合:データが正規分布に従わない可能性が高いです。例えば、上方または下方に弧を描くように曲がっている場合、分布の歪みや尖り(尖度)があると推測できます。
Q-Qプロットはデータの分布の形状を視覚的に確認するための強力なツールであり、特に大規模データセットに対して有効です。
3. 正規性検定
正規性検定は、データが統計的に正規分布に従うかどうかを評価するための統計的手法です。代表的な検定方法を以下に紹介します。
Shapiro-Wilk検定
Shapiro-Wilk検定は、小~中規模データセットで使用される正規性検定です。以下が手順です:
- 帰無仮説と対立仮説を立てます:
- 帰無仮説:データは正規分布に従う。
- 対立仮説:データは正規分布に従わない。
- p値の計算:Shapiro-Wilk検定によってp値が算出されます。
- p値が0.05未満であれば、帰無仮説は棄却され、データは正規分布に従わないと判断されます。
- p値が0.05以上であれば、正規分布に従っている可能性が高いと考えます。
Kolmogorov-Smirnov検定
Kolmogorov-Smirnov検定(K-S検定)は、データ分布が指定された理論分布(正規分布など)に従うかどうかを確認するために使います。Shapiro-Wilk検定よりも汎用的で、大規模なデータセットにも適しています。
- 帰無仮説と対立仮説:データが正規分布に従うかどうかを確認するための仮説を立てます。
- 結果の解釈:p値が0.05未満の場合、データは正規分布に従わない可能性が高いと判断されます。
Anderson-Darling検定
Anderson-Darling検定は、Shapiro-Wilk検定やK-S検定と同様、データが正規分布に従っているかを評価しますが、特に分布の端に敏感で、極端な値が影響するデータの検定に適しています。
- 帰無仮説:データは正規分布に従う。
- 結果の解釈:p値が基準を下回るとき、データが正規分布に従わないと判断します。
4. Jarque-Bera検定
Jarque-Bera検定は、正規分布に対するデータの歪度(Skewness)と尖度(Kurtosis)を評価する方法です。特に金融データの正規性確認などでよく使用されます。
- 歪度:データが平均からどれだけ左右に偏っているか
- 尖度:データの尖り具合
- Jarque-Bera検定のp値が小さい場合(通常0.05未満)、データが正規分布に従わないことを示します。
5. スケーリングや変換を活用した確認方法
データが正規分布に近づくよう、スケーリングや変換を行うことも有効です。こうした変換を行うと、正規性の確認が簡単になる場合があります。
- 対数変換:データが正の値のみである場合、対数を取ると正規分布に近づくことがあります。
- 平方根変換:元のデータの分布が偏っている場合、平方根変換によって正規性が改善されることがあります。
正規性検定の選択方法
| 検定名 | データ規模 | 特徴 |
|---|---|---|
| Shapiro-Wilk検定 | 小~中規模 | 正規分布専用。分布全体の形状に敏感。 |
| Kolmogorov-Smirnov検定 | 大規模データに対応 | 他の理論分布にも対応。 |
| Anderson-Darling検定 | 大規模~分布端の確認に有効 | 分布の端に敏感で、正規性の細部も確認可能。 |
| Jarque-Bera検定 | 中規模~特に金融データ | 歪度と尖度に基づく正規性検定。 |
まとめ:正規分布の特徴を活かしてデータを理解しよう
正規分布はデータの傾向を理解し、異常値の検出や品質管理などに応用される重要な概念です。分布の特性や応用を理解することで、データ分析の精度を高め、より深い洞察を得られるようになります。




