【データサイエンティスト検定】統計学の基礎：分散・標準偏差から正規分布までを体系的に理解する

統計学では、単に「平均」を見るだけでは不十分です。
データがどの程度ばらついているのか、どのような分布をしているのか を把握することが重要になります。

本記事では、

• 分散と標準偏差
• 四分位数とパーセンタイル
• 母集団と標本
• 不偏分散
• 正規分布と標準化

について、順を追って解説します。

---

1. データのばらつきを表す代表値

分散や標準偏差は、どちらも

データのばらつき（散らばり具合）

を表す代表的な統計量です。

一方で、

• 分布の左右の偏り
• データの位置関係

まで確認したい場合は、
四分位数やパーセンタイル を用います。

目的に応じて、これらの統計量を使い分けることが重要です。

---

2. 分散

定義

分散とは、

各データと平均値との差の2乗和の平均

を指します。

平均との差をそのまま足すと、正と負が打ち消し合ってしまうため、
2乗することで必ず正の値になるように しています。

---

分散の式

データを$$x_1, x_2, \dots, x_n$$x1​,x2​,…,xn​

平均を$$\bar{x}$$xˉ

とすると、分散は次の式で定義されます。$$\frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^2$$n1​i=1∑n​(xi​−xˉ)2

---

3. 標準偏差

定義

標準偏差とは、

分散の平方根を取った値

です。

分散は「2乗された単位」になっているため、
平方根を取ることで 元のデータと同じ単位 に戻します。

標準偏差は、

• s
• SD（Standard Deviation）

と表されます。

---

分散との関係

標準偏差は

分散を理解していれば自然に理解できる量

です。
計算式が複雑に見えても、実体は「分散の平方根」に過ぎません。

---

計算例

データ$$\{7, 9, 10, 11, 13\}$${7,9,10,11,13}

この平均値は 10 です。

データ	平均との差	差の2乗
7	-3	9
9	-1	1
10	0	0
11	1	1
13	3	9

• 差の2乗の合計：20
• 分散：20 ÷ 5 = 4
• 標準偏差：√4 = 2

したがって、

• 分散：4
• 標準偏差：2

となります。

---

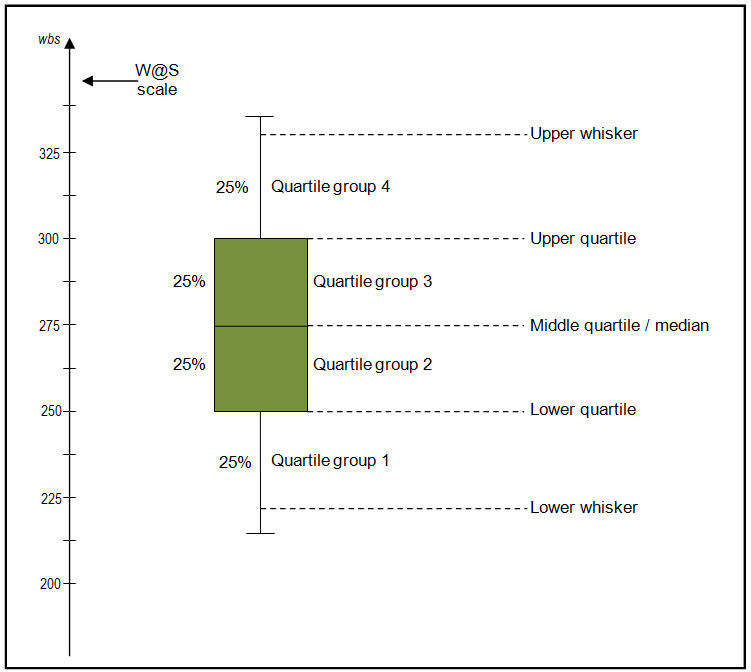
4. 四分位数

定義

四分位数とは、

データを小さい順に並べ、同じ件数ずつ4つに分けたときの区切りの値

です。

• 第1四分位数（Q1）
• 第2四分位数（Q2：中央値）
• 第3四分位数（Q3）

の3つがあります。

---

意味

四分位数を使うことで、

• データの散らばり具合
• 中央付近の集中度

を直感的に把握できます。

---

5. パーセンタイル

定義

パーセンタイルとは、

データを小さい順に並べたとき、全体の中で何％の位置にあるか

を表す指標です。

---

具体例

100人が背の低い順に並んだとき、

• 10パーセンタイル：前から10番目の人

を指します。

また、

• 25パーセンタイル → 第1四分位数
• 50パーセンタイル → 中央値
• 75パーセンタイル → 第3四分位数

に対応します。

---

6. 母集団と標本

母集団

母集団とは、

調査対象となるすべてのデータからなる集合

です。

例：

• 日本中のすべてのりんご
• 全国のすべての消費者

---

標本

標本とは、

母集団から抽出された一部のデータ

です。

実際の調査では、母集団すべてを調べることはほぼ不可能なため、
標本を分析して母集団の性質を推定 します。

---

7. 母平均と標本平均

• 母平均：母集団の平均
• 標本平均：標本の平均

母集団のサイズは非常に大きいため、
母平均を直接計算することは通常できません。

しかし、一定の条件のもとでは、

標本平均は母平均の良い推定値になる

ことが知られています。

---

8. 母分散・標本分散・不偏分散

標本分散の問題点

分散についても、

• 母集団の分散 → 母分散
• 標本の分散 → 標本分散

と区別されます。

ただし、標本分散は母分散より小さくなりやすい
という性質があります。

これは、母平均の代わりに 標本平均を使っている ことが原因です。

---

不偏分散

この過小評価を修正したものが 不偏分散 です。

不偏分散は、

母分散の推定値として用いられる分散

であり、次の式で定義されます。$$s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i – \bar{x})^2$$s2=n−11​i=1∑n​(xi​−xˉ)2

---

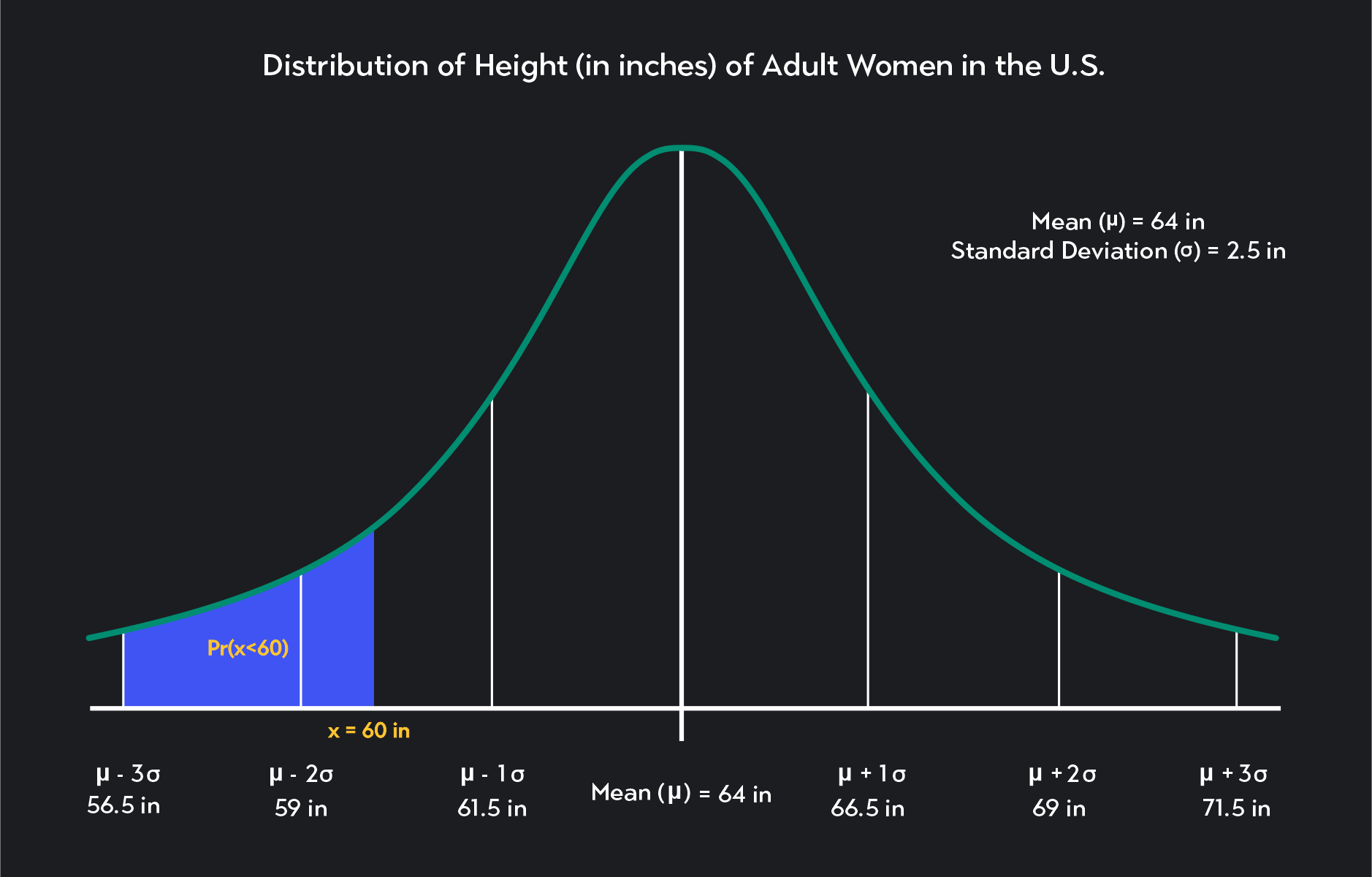
9. 正規分布

定義

正規分布とは、次の性質を持つ連続型確率分布です。

• 平均を中心に左右対称
• 山型の分布

理論的に扱いやすいため、
統計学・データ分析のさまざまな場面で利用されます。

---

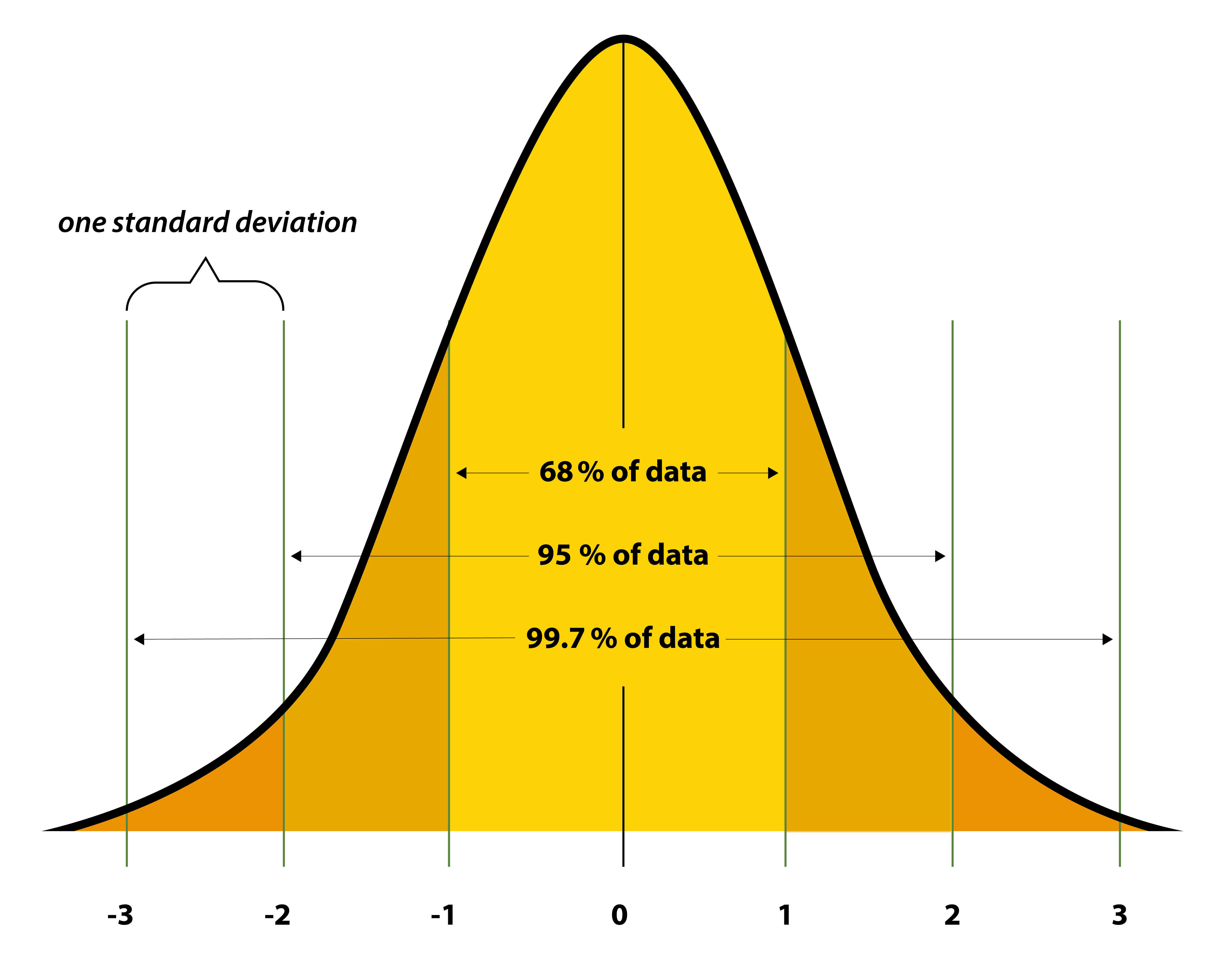
標準正規分布

標準正規分布とは、

• 平均：0
• 分散：1

の正規分布です。

---

10. 正規分布の標準化

正規分布に従う確率変数 X に対して、$$Z = \frac{X – \mu}{\sigma}$$Z=σX−μ​

という変換を行うことを 標準化 といいます。

このとき、

• Z は 標準正規分布 に従います。

標準化により、異なる尺度のデータ同士を
共通の基準で比較できるようになります。

---

まとめ

• 分散・標準偏差：データのばらつき
• 四分位数・パーセンタイル：分布の形や位置
• 母集団と標本：推定の前提
• 不偏分散：母分散の推定
• 正規分布・標準化：理論と応用の中心

これらはすべて、

統計的推定・検定・機械学習の前提となる基礎概念

です。