統計分析では、計算式を知ること以上に
「そのデータに何ができて、何ができないのか」 を理解することが重要です。
その判断基準となるのが 尺度(scale) です。
尺度とは、本項目では 「データの種類」 と考えるとよいでしょう。
本記事では、
- データの尺度の分類
- 尺度ごとに可能な統計処理
- 相関係数の意味と注意点
について解説します。
目次
1. データの尺度とは何か
私たちが収集するデータは、大きく次の2つに分けられます。
- 量的データ
- 質的データ
尺度を誤解すると、意味のない平均や相関を計算してしまう 危険があります。
2. 量的データ
定義
量的データとは、
数値そのものに意味があり、足し算や引き算ができるデータ
です。
量的データには、平均値・分散・相関係数など
多くの統計量を適用できます。
量的データは、さらに次の2つに分類されます。
2.1 比例尺度(Ratio Scale)
比例尺度とは、
絶対的なゼロ点を持つ尺度
です。
例:
- 長さ
- 質量
- 絶対温度(K)
- 価格
比例尺度では、
- 平均
- 差
- 倍率(2倍、半分など)
すべてに意味があります。
2.2 間隔尺度(Interval Scale)
間隔尺度は、
絶対的なゼロ点を持たない尺度
です。
代表例は 摂氏温度(℃) です。
- 0℃は「温度が存在しない」わけではない
- あくまで基準点が定められているだけ
そのため、
- 差(20℃ − 10℃)は意味がある
- 倍率(20℃は10℃の2倍暑い)は意味がない
という点に注意が必要です。
3. 質的データ
定義
質的データとは、
分類や種類を区別するためのラベルとしてのデータ
です。
質的データでは、
- 和
- 差
- 平均
といった計算は 意味を持ちません。
質的データは次の2つに分かれます。
3.1 順序尺度(Ordinal Scale)
順序尺度とは、
大小関係のみが意味を持つデータ
です。
例:
- 満足度(★1~★5)
- 等級(A・B・C)
- ランキング
順序は比較できますが、
間隔が等しいとは限らない ため、通常は平均値に意味がありません。
3.2 名義尺度(Nominal Scale)
名義尺度とは、
区別のためだけに数値が割り当てられたデータ
です。
例:
- 性別(男性=0、女性=1)
- 子ども=0、成人=1
名義尺度では、
- 等しいかどうか(=)のみが比較可能
です。
4. 尺度を誤ると起こる問題
尺度によって 使用可能な統計手法は異なります。
たとえば、
- データサイエンティストスキルチェックが
★1~★3 の順序尺度で評価されている場合
会社A:★1 が3名
会社B:★3 が1名、★0 が2名
いずれも平均は ★1 になりますが、
実力が同じと結論付けるのは不適切 です。
これは、
- 順序尺度に
- 比例尺度向けの平均を使っている
ことが原因です。
5. 相関係数とは何か
相関係数とは、
2つの変数が線形(直線)で表せるような関係を持つか
その強さを数値で表した指標
です。
相関係数を用いることで、
データ間の関係性を簡潔に把握できます。
6. ピアソンの積率相関係数
相関係数には複数の種類がありますが、
ここでは ピアソンの積率相関係数 を扱います。
使用できるデータ
ピアソンの相関係数は、
- 量的データ
- 比例尺度
- 間隔尺度
にのみ適用可能です。
- 順序尺度
- 名義尺度
には使用できません。
定義式の意味
相関係数 rxy は、
- Sx:x の標準偏差
- Sy:y の標準偏差
- Sxy:共分散
を用いて定義されます。
共分散は、
x と y が同時にどの方向に変動するか
を表す量です。
7. 相関係数の値の解釈
相関係数は −1 ~ 1 の値を取ります。
- 正の値
- x が大きいほど y も大きくなる
- 正の相関
- 負の値
- x が大きいほど y は小さくなる
- 負の相関
- 0
- 線形な関係がない
- 無相関
| 相関係数 | 解釈 |
|---|---|
| ±1 に近い | 強い相関 |
| 中程度 | 弱い相関 |
| 0 | 無相関 |
8. 具体例:気温とアイスクリームの売上
例として、
- 1日の平均気温
- アイスクリームの売上
の疑似データを用いて相関係数を計算すると、
- 相関係数:0.953
となります。
これは、
気温が高くなるほど、アイスクリームの売上が増える
という 強い正の相関 を示しています。
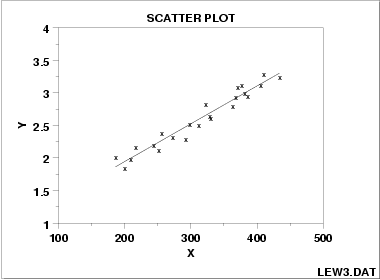
9. 相関係数の注意点
重要な注意点として、
相関係数の絶対値が大きくても、因果関係があるとは限らない
ことが知られています。
また、
- 非線形な関係
- 外れ値の影響
によって、相関係数が誤解を招く場合もあります。
そのため、
相関係数だけで判断せず、散布図も必ず確認する
ことが望ましいです。


まとめ
- 尺度は「データの種類」を表す重要概念
- 尺度により使える統計手法は異なる
- 相関係数は量的データのみで計算可能
- 相関係数は関係の強さを示すが、因果は示さない
- 散布図と併用して解釈することが重要
尺度の理解は、
正しい統計分析を行うための出発点
です。


