統計学は大きく分けて 記述統計学 と 推測統計学 の2つから構成されます。
データサイエンティスト検定™ リテラシーレベルでは、この違いと役割を正しく理解していることが重要です。
本記事では、
- 記述統計学と推測統計学
- 点推定・区間推定
- 仮説検定の考え方と手順
- 有意水準・p値・検定力
- t検定の使い分け
- 共起性とアソシエーション分析
について、体系的に解説します。
目次
1. 記述統計学と推測統計学
記述統計学
記述統計学とは、
特定の集団から得られたデータを
表・グラフ・統計量によって整理・要約し、考察する手法
です。
用いられる代表例:
- 平均・分散・標準偏差
- 相関係数
- ヒストグラム・箱ひげ図
記述統計学は、**「今、手元にあるデータそのもの」**を説明するための統計です。
推測統計学
推測統計学とは、
無作為に抽出した標本(サンプル)を手がかりに
母集団の性質を推測する統計学
です。
例:
- 視聴率
- 選挙の当選確率
- 世論調査
母集団が非常に大きく、全数調査が困難な場合に用いられます。
2. 推定:点推定と区間推定
点推定
点推定とは、
母集団の特性を、1つの値で推定する方法
です。
例:
- 標本平均を母平均の推定値とする
ただし、点推定では 推定誤差の大きさが分からない という欠点があります。
区間推定
区間推定とは、
母集団の値が含まれると考えられる区間で推定する方法
です。
- 推定区間:(A,B)
- 母集団の値がその区間に含まれる確率
→ 信頼度(信頼水準・信頼係数)
よく使われる信頼度:
- 90%
- 95%
- 99%
信頼区間の解釈
- 同じ信頼度で
- 区間が 広い → 推定精度が低い
- 区間が 狭い → 推定精度が高い
という意味になります。
3. 仮説検定とは何か
検定とは、
母集団について立てた仮説が正しいかどうかを
標本データを用いて確率的に判断する方法
です。
母集団の全データが分かっていれば検定は不要ですが、
実務ではほとんどの場合、標本しか得られません。
4. 仮説検定の基本構造
仮説検定は、次の考え方に基づきます。
- 帰無仮説を立てる
- 対立仮説を立てる
- 帰無仮説が正しいとしたら
「今回の結果はどれほど珍しいか」を調べる
帰無仮説と対立仮説
例:サイコロの3の目が怪しい場合
- 帰無仮説(H₀)
- 「3の目が出る確率は 1/6 である」
- 対立仮説(H₁)
- 「3の目が出る確率は 1/6 ではない」
帰無仮説が成立するとは考えにくい場合、
帰無仮説を棄却し、対立仮説を採択します。
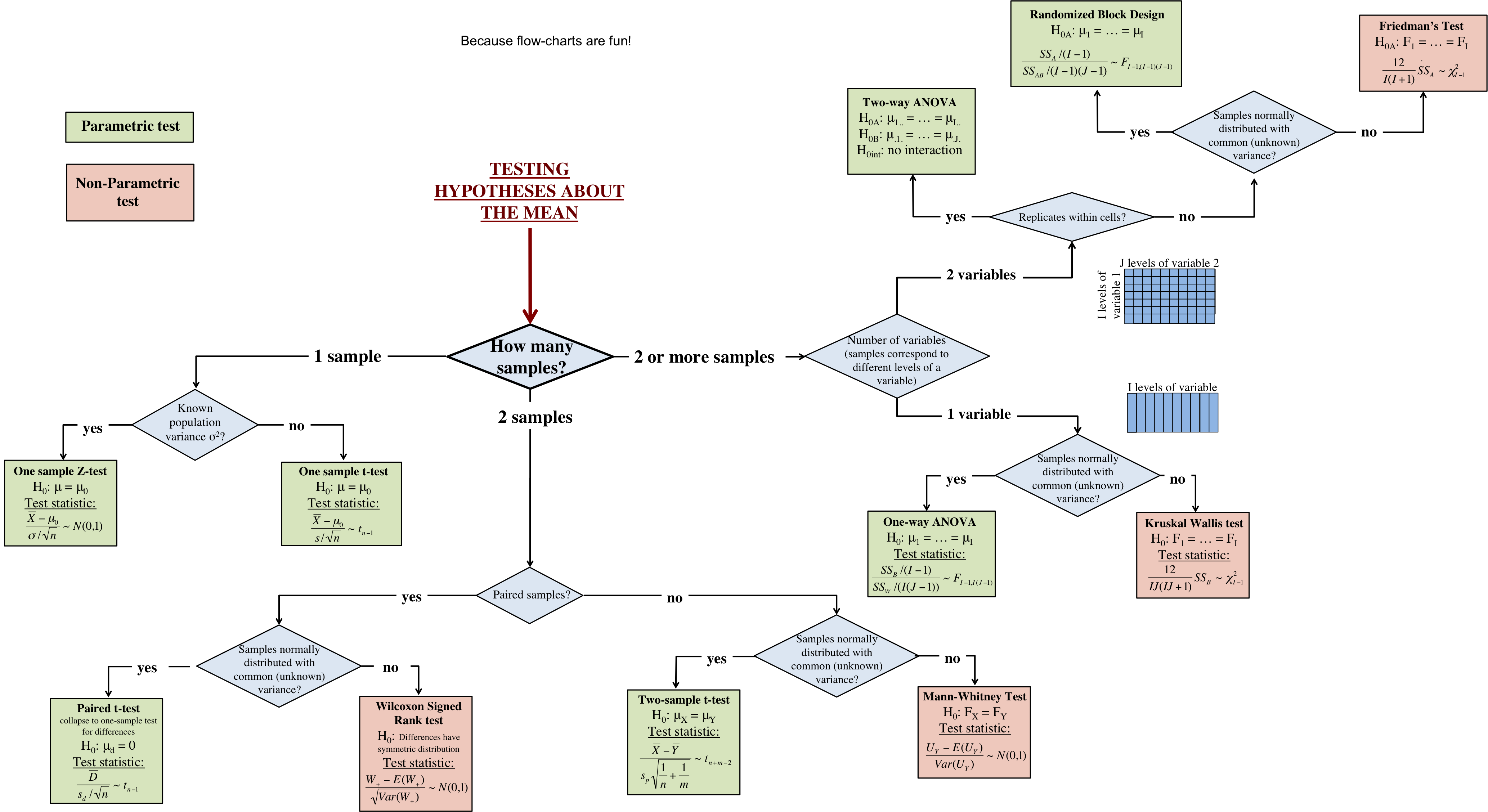

5. 有意水準と p 値
有意水準
有意水準とは、
「これ以下の確率なら、偶然とは考えにくい」と判断する基準
です。
慣例的に:
- 5%
- 1%
がよく使われます。
p値
p値とは、
帰無仮説が正しいと仮定したとき、
観測された統計量以上に極端な結果が出る確率
です。
- p値 < 有意水準 → 帰無仮説を棄却
- p値 ≥ 有意水準 → 帰無仮説を棄却できない
6. 第1種の過誤と第2種の過誤
仮説検定は確率的判断であるため、誤りの可能性があります。
| 種類 | 内容 |
|---|---|
| 第1種の過誤 | 帰無仮説が正しいのに棄却 |
| 第2種の過誤 | 帰無仮説が誤りなのに棄却できない |
- 第2種の過誤の確率:β
- 検定力:1 − β
検定力が低い検定は、実務では注意が必要です。
7. 片側検定と両側検定
対立仮説の立て方により、検定は次の2つに分かれます。
両側検定
- 「等しくない」
- 例:表の確率 ≠ 0.5
片側検定
- 「大きい」「小さい」
- 例:表の確率 > 0.5
対立仮説の設定により、棄却域が大きく変わるため、
検定の種類を必ず意識する必要があります。
8. 2群の平均値の差の検定(t検定)
対応があるデータ
例:
- ダイエット前後の体重
→ 同一対象なので 対応あり
- 1標本の検定と同様に扱う
- 差が0かどうかを検定
対応がないデータ
例:
- A組とB組の平均点
→ 異なる対象なので 対応なし
- 2標本 t 検定を使用
- 自由度:nA+nB−2
t検定の種類
- スチューデントの t 検定
- 等分散を仮定
- ウェルチの t 検定
- 分散が異なる場合
等分散かどうかは F検定 で確認します。
9. 共起性とアソシエーション分析
共起頻度
共起頻度とは、
2つの事象が同時に起こる回数
です。
関係性を測る指標
| 指標 | 意味 |
|---|---|
| 支持度 | 全体に占める共起の割合 |
| 信頼度 | X が起きたとき Y が起きる割合 |
| リフト値 | 条件付き確率がどれだけ高まるか |

アソシエーション分析とレコメンド
これらの指標は、
- アソシエーション分析
- 教師なし学習
で利用されます。
代表例:
- 「Xを買った人はYも買っている」
ただし、レコメンドでは 方向性(X→Y) が重要です。
まとめ
- 統計学は記述統計と推測統計に分かれる
- 推測統計には推定と検定がある
- 仮説検定は帰無仮説を棄却できるかを見る手法
- 有意水準・p値・検定力の理解が重要
- t検定はデータの性質により使い分ける
- 共起・アソシエーション分析は実務に直結
本記事で扱った内容は、
データサイエンティスト検定™ リテラシーレベルの中核であり、
実務・試験の両方で必須の知識です。


