データ分析では「差があるのか？」を検証する場面と、「一緒に起きやすいパターン」を発見する場面が頻出です。
前者は 仮説検定（平均差の検定）、後者は 共起分析（アソシエーション分析） が代表的なアプローチです。

本記事では、

1. 2群の平均値の差の検定（対応あり／なし、t検定／z検定、等分散／不等分散）
2. 共起頻度・支持度・信頼度・リフト値（レコメンドへの応用）
   を体系的に整理します。

---

1. 2群の平均値の差の検定が「ポピュラー」な理由

ビジネスでも研究でも、「施策の効果があったか」「AとBに差があるか」を確かめたいケースが多くあります。

• ダイエットプログラム前後で体重が変化したか
• A組とB組で平均点に差があるか
• 広告クリエイティブAとBでCVRに差があるか（平均の差として扱う例）

このとき重要なのが、データの取り方によって適切な検定が変わる点です。

---

2. まず押さえる：対応があるデータ／対応がないデータ

2.1 対応があるデータ（paired）

同じ対象を「前後」で測っているケースです。

• 例：同じ人の「施策前の体重」と「施策後の体重」

この2つのデータは「同一人物」に紐づいており、個人差が揃っているため、差分に着目できます。
つまり、「2標本」ですが実質は 差分の1標本問題 になります。

---

2.2 対応がないデータ（independent）

異なる対象から抽出された2群を比べるケースです。

• 例：A組とB組（別の児童集団）
• 例：別ユーザー群に広告A/Bを見せた結果

この場合、2群は独立にサンプルされているため、2標本の平均差として扱います。

---

3. 対応がある場合：対応のある t 検定（差分で1標本）

3.1 仮説の立て方

差分 $d_i = \text{(後)} – \text{(前)}$di​=(後)−(前) を作り、平均との差を検定します。

• 帰無仮説 H0H_0H0​：平均との差は0（前後で変化なし）
  • 「前後の体重の差は0である」
• 対立仮説 H1H_1H1​：
  • 両側検定：「差は0ではない」
  • 片側検定：「体重が減った」など方向を持つ（例：差 > 0 / 差 < 0）

3.2 検定統計量（基本形）

母集団が正規分布に従う（または差分が概ね正規）と仮定し、$$T = \frac{\bar{d} – 0}{s_d / \sqrt{n}}$$T=sd​/n​dˉ−0​

• $\bar{d}$dˉ：差分の平均
• $s_d$sd​：差分の標準偏差
• 自由度：n−1n-1n−1
• $T$T は t分布（自由度 n−1n-1n−1） に従う

5%水準などで棄却域に入るか（またはp値）で判断します。

---

4. 対応がない場合：独立2標本の t 検定

4.1 仮説

• 帰無仮説 H0H_0H0​：A組とB組の平均は等しい（平均差=0）
• 対立仮説 H1H_1H1​：平均に差がある（平均差≠0）
  → 多くは 両側検定 を採用します。

---

4.2 等分散を仮定：スチューデントの t 検定

「2群の母分散が等しい」という前提で、分散をプールして t を作ります。

• 自由度：nA+nB−2n_A + n_B – 2nA​+nB​−2
• この前提が怪しいときは次のウェルチへ。

---

4.3 不等分散：ウェルチの t 検定

2群の分散が異なる可能性がある場合に用います。
実務ではウェルチをデフォルトにする流儀も多いです（特に標本数や分散が偏りやすいデータ）。

---

5. 等分散かどうか：F検定と注意点

等分散かを調べるために F検定 を行う、という流れが教科書的に紹介されます。
F検定は分散分析（ANOVA）にも繋がる重要な検定です。

ただし実務では、

• 正規性の仮定に敏感
• 事前の等分散判定がかえって不安定
  などの理由から、最初からウェルチを採用するケースもあります。
  （試験では「等分散→スチューデント」「不等分散→ウェルチ」「等分散判定→F検定」を整理して覚えるのが安全です。）

---

6. 母分散が既知なら：z検定

t検定は 母分散が未知 であることを前提とします。
もし母分散が既知（現実には稀）なら、標準化して z検定 を用います。

---

7. 学習ポイントまとめ（検定パート）

• 「対応あり」は 差分を取って1標本 として考える
• 「対応なし」は 独立2標本 として考える
• 等分散ならスチューデント、不等分散ならウェルチ
• 有意水準・p値・片側/両側の設定で結論が変わる

---

8. 共起分析：共起頻度→Support/Confidence/Lift

次に、「データに潜むパターン」を見つける文脈で重要な 共起性・関係性 を扱います。
ECやメディア、広告でも「一緒に起きやすい行動」を掴むのは定番です。

---

8.1 共起頻度（co-occurrence count）

共起頻度とは、

2つの事象が同時に起きている回数（件数）

です。
例：同一注文内で「XとYが一緒に買われた件数」

---

8.2 支持度（Support）

支持度は、

全体のうち、XとYが同時に起こる割合

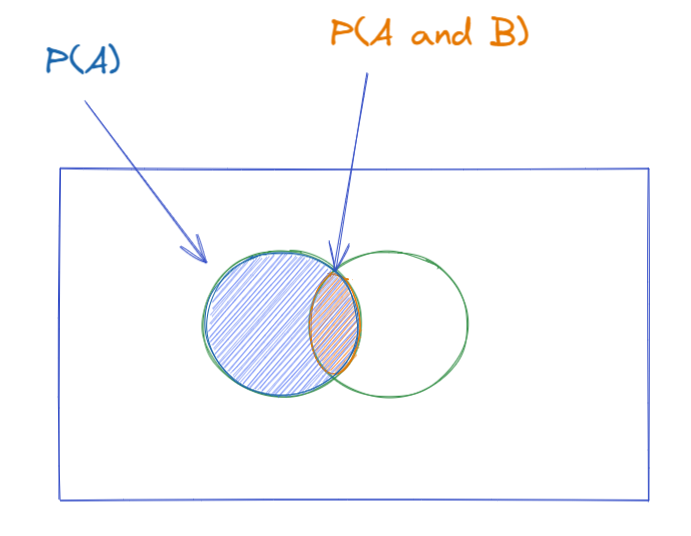
$$\text{Support}(X, Y) = P(X \cap Y)$$Support(X,Y)=P(X∩Y)

「そのルールがどれだけ一般的か（母数に対する頻度）」を示します。

---

8.3 信頼度（Confidence）

信頼度は、

Xが起きた条件の下で、Yが起こる割合

$$\text{Confidence}(X \rightarrow Y) = P(Y \mid X)$$Confidence(X→Y)=P(Y∣X)

結びつきの強さを表す最も素直な指標です。

---

8.4 リフト値（Lift）

リフト値は、

Xが起きたときにYが起こる確率が、
何も条件がないときのYの確率よりどれくらい高いか

$$\text{Lift}(X \rightarrow Y) = \frac{P(Y \mid X)}{P(Y)}$$Lift(X→Y)=P(Y)P(Y∣X)​

• Lift > 1：XがあるとYが起きやすい
• Lift = 1：独立に近い
• Lift < 1：XがあるとYが起きにくい

---

---

9. アソシエーション分析とレコメンドの「方向性」

Support/Confidence/Lift は、アソシエーション分析（教師なし学習の一種）でよく使われます。
代表例が「バスケット分析（Market Basket Analysis）」です。

重要なのは、レコメンドでは 方向性（X→Y） が意味を持つことです。

• 共起頻度：XとYは入れ替え可能（対称）
• ルール（レコメンド）：X→Yは非対称（方向あり）

例：シリーズ本

• 上巻 → 下巻 は自然な推薦
• 下巻 → 上巻 はデータ上は起こっても、推薦として不自然な場合がある

つまり、指標が高いだけで採用せず、

• ドメイン知識
• 取得データの背景
• 方向性の妥当性
• ビジネス上の意味

も合わせて「価値あるルール」を選別する必要があります。

---

まとめ

平均差の検定（t検定/z検定）

• 対応あり：差分にして1標本（自由度 $n-1$n−1）
• 対応なし：独立2標本（自由度は条件で変化）
• 等分散→スチューデント、不等分散→ウェルチ
• 母分散既知→z検定（現実には稀）

共起分析（Support/Confidence/Lift）

• 共起頻度：同時発生の件数
• 支持度：共起の割合
• 信頼度：条件付き確率 $P(Y|X)$P(Y∣X)
• リフト：上振れ度合い $\frac{P(Y|X)}{P(Y)}$P(Y)P(Y∣X)​
• レコメンドでは 方向性と文脈 が必須