z検定とt検定の使い分け

始めに

統計学では、サンプルから母集団についての推測を行う際に、z検定やt検定といった手法を用います。これらの検定方法はどちらも平均値の比較に使われますが、適用する場面には違いがあります。この記事では、z検定とt検定の違いや、どのような場合にそれぞれを使うべきかを解説します。

1. z検定とは

z検定は、母集団の標準偏差が既知の場合に使用される検定です。通常、サンプルサイズが大きい場合（一般的には30以上）が推奨されます。これは、サンプルサイズが大きいほど、サンプル平均が正規分布に従うという中心極限定理が働くためです。

z検定が適している場合：

母集団の標準偏差がわかっている。
サンプルサイズが十分に大きい（n ≥ 30）。

z検定の例：

例えば、製品の生産ラインで、過去のデータから製品の品質における標準偏差が既知であるとします。この場合、新しいサンプルの平均と目標値の比較にz検定が使用されます。

2. t検定とは

t検定は、母集団の標準偏差が不明な場合に使用されます。また、サンプルサイズが小さい場合（n < 30）でもt検定が適用されます。

t分布は、標本サイズが小さい場合に不確実性を考慮しているため、z分布（標準正規分布）とは形が異なり、サンプル数が増えるとz分布に近づきます。

t検定が適している場合：

母集団の標準偏差がわからない。
サンプルサイズが小さい（n < 30）。

t検定の例：

例えば、小規模な調査で少数の被験者を対象に、新しい教育プログラムの効果を評価する場合、母集団の標準偏差が不明であり、サンプルサイズも少ないため、t検定が適しています。

3. z検定とt検定の計算式

自由度とは何か？

自由度は、データの独立した情報量を表します。簡単に言えば、「データが自由に変動できる数」と考えることができます。

例:
5つの数値の平均を計算した後、そのうち4つの数値を自由に選べますが、5つ目の値は平均を保つために決まります。この場合、自由度は「5 − 1 = 4」です。

z検定とt検定の使い分けにおける自由度の重要性

自由度は、z検定とt検定の選択に影響を与える要因の一つです。

z検定:
- 母集団の標準偏差が既知で、標本サイズが大きい場合。
- 自由度は関係ありません。
t検定:
- 母集団の標準偏差が未知で、標本サイズが小さい場合。
- 自由度がサンプルサイズに影響し、t分布の形状を決定します。自由度が大きいほど、t分布はz分布（標準正規分布）に近づきます。

t検定での自由度の計算方法

1. 片標本t検定の場合

自由度=n−1

n: サンプルサイズ。

2. 独立二標本t検定の場合

自由度=(n₁−1)+(n₂−1)=n₁+n₂−2

n1,n2: 各サンプルのサイズ。

3. 対応のあるt検定（対応のある標本の場合）

自由度=n−1

n: ペアの数。

自由度が検定結果に与える影響

自由度が小さい場合、t分布の裾（端の部分）が厚くなり、標本平均の変動を大きく考慮します。
自由度が大きくなるほど、t分布はz分布に近づきます。標本サイズが十分大きければ、t検定でもz分布を近似として使用できます。

4. z検定とt検定の計算式

z検定とt検定は似た構造を持っていますが、計算に使用する分布が異なります。

z検定の統計量

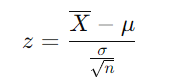
Xはサンプル平均、μは母集団の平均、σは母集団の標準偏差、nはサンプルサイズです。

t検定の統計量

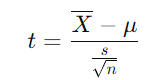
ここで、sはサンプルの標準偏差です。

5. 実際の使い分けのポイント

サンプルサイズ

サンプルサイズが大きい場合（一般的にn ≥ 30）、z検定が適用されやすいです。これは、サンプルサイズが大きくなると、サンプル平均が正規分布に近づくためです。母集団の標準偏差が既知の場合は、z検定を使用することで、より精度の高い推定が可能です。
一方で、小さいサンプルサイズ（n < 30）の場合、t検定を使用します。t分布はサンプル数が少ない状況でも信頼区間を正確に計算できるように調整されており、t検定はこの小規模サンプルに適しています。

例えば、小規模の調査では、サンプル数が10〜20程度の場合が多く、この状況ではt検定が適切です。企業内の限られた従業員に対して新しいトレーニングプログラムの効果を測定する場合も、サンプルが小さいためt検定を選びます。逆に、大規模な調査や生産ラインにおける日常的な製品検査のように、データが豊富な場合はz検定を使います。

母集団の標準偏差

母集団の標準偏差が既知かどうかも重要な要素です。標準偏差が既知の場合、z検定が推奨されます。例えば、過去の大量のデータを使って製品のばらつきが安定していると分かっている場合、母集団の標準偏差を利用してz検定を実行することでより精度の高い結果が得られます。

一方で、標準偏差が不明な場合、サンプルから推定した標準偏差を使ってt検定を行います。このような状況では、標本のバラつきに対して、t分布がより柔軟に対応できるため、特にサンプルサイズが小さい場合に有効です。たとえば、まだデータが限られている新製品のテストや、新たに収集された市場調査データでは、母集団の標準偏差を直接知ることは難しいため、t検定が適用されます。

6. z検定とt検定の共通点

仮説検定の基本的な流れ

両者ともに仮説検定のフレームワークに従います。基本的な流れとしては、まず**帰無仮説（H₀）と対立仮説（H₁）**を設定し、標本データに基づいて統計量（z値またはt値）を計算し、対応する分布を使ってp値を求めます。このp値を基にして、通常5%の有意水準と比較し、帰無仮説を棄却するかどうかを判断します。

例えば、ある新薬の効果を検証する際に、「新薬は既存薬と同じ効果を持つ」（帰無仮説）と、「新薬は既存薬よりも効果が高い」（対立仮説）という2つの仮説を立てます。これに対してサンプルデータからz値やt値を算出し、p値が5%未満であれば、対立仮説を採択し、新薬がより効果的であると判断します。

標本平均と母平均の比較

両方の検定とも、標本平均と母集団平均の比較を行います。標本平均が母集団平均からどれだけ離れているかを数値的に示すのがz値やt値です。統計的に意味のある差があるかどうかを判断するために、z検定またはt検定を使って、この差が偶然によるものかどうかを評価します。

たとえば、ある製品の平均寿命を従来品と比較する場合、標本データから新しい製品の平均寿命を計算し、それが従来品の平均寿命とどれくらい違うかをz検定またはt検定で評価します。この際、標本サイズや母集団の標準偏差が既知かどうかに応じて、適切な検定手法を選択します。

7. まとめ

z検定とt検定は、どちらも平均の差を評価する重要な手法ですが、サンプルサイズや母集団の標準偏差の既知/未知によって使い分けが必要です。適切な検定方法を選択することで、より正確な結論を導き出すことができます。

始めに