統計について学ぶ際に、『95%信頼区間』であったりp<0.05という表現を必ず耳にしたり目にします。
教科書通りに理解を進めていく中だとなかなか気づきにくい部分ではありますが、例えばp<0.05という結果が出た時の受け止め方としては、『統計における有意差がある』と思います。
ただ、一度俯瞰的に見ると有意差あり(p<0.05)と判断はしているものの、実際の現場だと有意差がないケースも発生することがあります。
それらの、統計と現場における差異を示すのが第1種の過誤と第2種の過誤というものです。
これらは非常に重要な項目であるのでしっかりとインプットいただくのが良いかと思います。
第1種の過誤
第1種の過誤とは
まずはじめに第1種の過誤から解説します。
第1種の過誤とは結論から言うと、本当は有意差がないのに統計によって有意差があると判断してしまうことです。
以前二項検定について解説している記事で使った医薬品の例を使います。
二項検定を分かりやすく解説!
例題として
医薬品Aの有効率=0.6
医薬品Bの有効率=0.2
であったときの二項検定を行います。
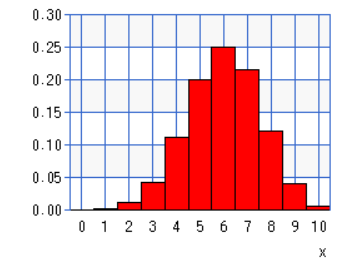
医薬品Bの有効率は0.2のため、10人に投与した場合の有効だった人数は2人になります。
その場合x=2となり、
左側の棄却域(2.5%)に入ります。
その結果、判断としては帰無仮説は棄却され(比べる者同士は異なる)「有意差ありp<0.05」となります。
わざわざ二項検定を行うまでもなく、医薬品AとBは有意差があると判断できます。
では次に、もし医薬品AとBが同じ有効率を示すとします。
その場合、間違いなく帰無仮説は正しいとされ比べる者同士は等しいはずです。
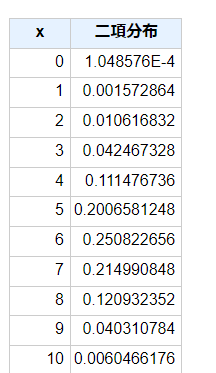
有効率0.6の場合の確率分布は

となり、それぞれの確率は

となります。
有意差の判断を行うにあたり、棄却域を設定しますがその確率は以前の記事で紹介したように95%でした。
これは、もし帰無仮説が正しいのであれば、95%の確率で有意差なしという正しい判断が下せるということを意味してます。
改めてになりますが、今回医薬品AとBが同じ有効率を示すと定義しました。
これは違和感があると思います。
医薬品AとBは同じ有効率だといっているのに5%の確率で棄却されるのです。
初めに示した➀医薬品A(有効率0.6)とB(有効率0.2)と次に示した➁医薬品A(有効率0.6)とB(有効率0.6)が同じもので、真実は医薬品AとBの有効率はともに0.6だった場合、➀は医薬品Bになにかしらの事案が発生して有効率が0.2だったのかもしれません。
ただ、真実は医薬品AとBの有効率は同じだった(=帰無仮説は正しい)ので、5%の確率で➀の有意差ありが起きてしまいました。
真実は『帰無仮説が正しい』にもかかわらず、有意差ありと判断してしまうことが第1種の過誤です。
ただ、第1種の過誤が起こる確率は一定で、棄却域の確率がそのまま起こる確率になります。
第1種の過誤の例
・ある「血圧を下げる効果がある」健康食品があった場合,本当は効果がない場合に「血圧が下がる効果がある」と判断する
・広告クリエイティブを配信した際、本当はコンバージョンレートに差がないのに差があると判断する
・コロナの検査を行ったとき、本当は陰性(健常人と同じ)なのに陽性と判断してしまう(偽陽性)
第2種の過誤
第2種の過誤とは
次に第2種の過誤について解説します。
第2種の過誤についても結論から言うと、本当は有意差があるのに統計によって有意差がないと判断してしまうことです。
詳しく解説するために、同じように二項検定について解説している記事で使った医薬品の例を使います。
二項検定を分かりやすく解説!
例題では
医薬品Aの有効率=0.6
医薬品Bの有効率=0.4
で結果的に帰無仮説は棄却されないという結論に至りました。
つまり帰無仮説は正しいという判断です。
ここでみなさんの直感に問いかけたいのですが、有効率0.6と0.4の医薬品は差がないと言えるでしょうか?
直感的に考えると二つの薬には効果の差があると考えないでしょうか?
例題に戻り、有効率0.6の確率分布をお示しします。
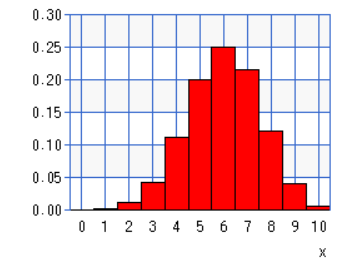
この場合の棄却域は下の表で見るとピンクの部分です。
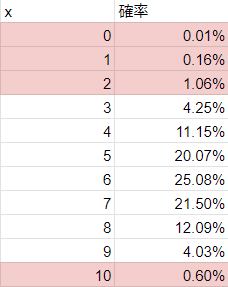
これに医薬品B(有効率0.4)の確率分布を重ね、医薬品Aにおける棄却域にBが何%入るのか計算します。
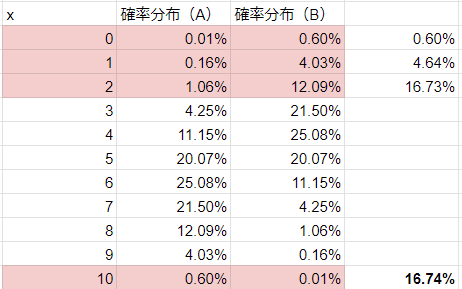
Bにおけるピンクの部分の確率を足し上げると、16.74%になります。
これは16.74%の確率で医薬品AとBは有意差がある(異なる薬剤)と判断され、83.26%の確率で有意差なしと判断されます。
当初例題においては医薬品AとBは有意差なしという判断を行いました。
しかし実際のところ、その判断の確率は8割ほどで残りの2割弱の確率で違う有効率だと判断します。
これが第2種の過誤であり、第1種の過誤と比べてもその確率は変化します。
第2種の過誤の例
・ある「血圧を下げる効果がある」健康食品があった場合,本当は効果があるのに「血圧が下がる効果がない」と判断する
・広告クリエイティブを配信した際、本当はクリック率に差があるのに差がないと判断する
・コロナの検査を行ったとき、本当は陽性なのに陰性と判断してしまう(偽陰性)