1. 決定係数とは?
- 定義:
決定係数(coefficient of determination)は、統計学や機械学習において、モデルの予測精度を評価するための指標です。通常、R2 と表記され、0から1の値を取ります。値が1に近いほど、モデルがデータの分散をよく説明していることを意味します。 - 数式:
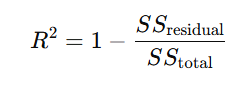
- SSresidual: 残差平方和
- SStotal: 全変動の平方和
2. 決定係数の解釈
- 値の範囲と解釈:
- R2=1: モデルがデータを完全に説明。
- R2=0: モデルがデータを全く説明していない。
- 負の値: モデルが平均値による予測よりも悪い場合(特殊な場合)。
- 実例:
住宅価格を予測するモデルで R2=0.8 の場合、80%の変動がモデルで説明可能であり、残り20%は説明できないことを意味します。
3. 決定係数の計算例
- データ例:
- 実測値: [100, 150, 200]
- 予測値: [110, 145, 195]
- ステップ:
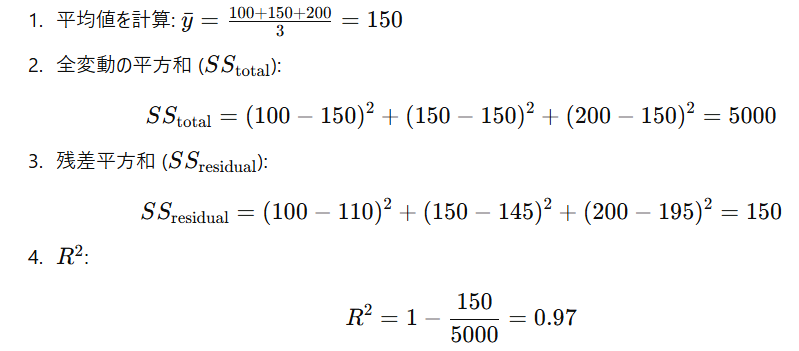
- 解釈: モデルは97%の変動を説明しています。
4. 決定係数の限界
- 高い R2R^2R2 が必ずしも良いモデルを意味しない:
- 過学習(overfitting)の可能性。学習データに特化しすぎると、テストデータでは低い精度になる場合があります。
- 非線形モデルでは不適切な場合も:
線形回帰には適用されますが、非線形回帰や分類問題では別の指標(AUCやF1スコアなど)のほうが適切です。
5. 決定係数以外の評価指標
- 調整済み決定係数:
説明変数が多い場合、モデルの複雑さを考慮して評価する指標。
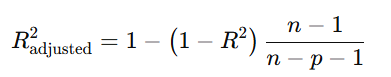
- n: データ数
- p: 説明変数の数
- 他の指標:
- RMSE(Root Mean Square Error)
- MAE(Mean Absolute Error)
6. 統計学や機械学習での実践例
- 線形回帰モデルでの使用:
「宣伝費と売上の関係」など、連続変数を扱うケースで利用される。 - 注意点:
時系列データや分類問題では不適切な場合があるため、データの特性に応じた指標選びが重要。
7. まとめ
- 決定係数は回帰モデルの性能をシンプルに評価するための有用な指標。
- 解釈には注意が必要であり、特に過学習やデータの特性を無視しないことが重要。
- 他の評価指標と併用することで、モデルの性能をより正確に把握可能。




