マンホイットニーのU検定（Mann-Whitney U Test）は、2つの独立したグループの分布が同じかどうかを検定するための非パラメトリック手法です。特に、データが正規分布に従わない場合やサンプルサイズが小さい場合に役立ちます。この検定は、ウィルコクソンの順位和検定（Wilcoxon Rank-Sum Test）とも呼ばれます。
目次
マンホイットニーのU検定を使う場面
マンホイットニーのU検定が使われる具体的なシチュエーションを以下に挙げます：
- 薬剤の効果を比較: 新薬Aと従来薬Bの患者グループ間で血圧の変化量に差があるか検討する。
- 教育の効果測定: 2つの異なる教育プログラムを受けた生徒の試験スコアを比較する。
- ウェブサイトのUIテスト: 異なるデザインのランディングページAとBで、滞在時間に差があるかを検証する。
これらの場合、データが正規分布していない場合や、外れ値の影響を受けやすい場合に特に有用です。
検定の背景と考え方
マンホイットニーのU検定は、以下のようなステップで行われます：
- データの順位付け: 2つのグループのデータを結合して小さい順に並べ、順位を付けます。
- 順位の合計を求める: 各グループの順位の合計値を計算します。
- U統計量を計算: 次の式でU統計量を求めます：
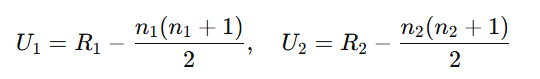
- R1,R2 は各グループの順位の合計、n1,n2 はそれぞれのグループのサンプルサイズです。
- 小さい方のU値を選ぶ: U=min(U1,U2)
- 有意性の評価: 計算されたU値を基に、帰無仮説を棄却するかどうかを判断します。
仮説の設定
マンホイットニーのU検定では、統計学における標準的な仮説設定を行います。具体的には以下のように設定されます：
帰無仮説 (H0)
「2つの独立したグループの分布は同一である」と仮定します。つまり、グループ1とグループ2が同じ母集団からのサンプルである場合、データの分布に違いがないことを意味します。
対立仮説 (H1)
「2つの独立したグループの分布は異なる」と仮定します。具体的には、以下のように考えられます：
- 両側検定: グループ1とグループ2の分布が異なる（どちらが大きいか指定しない）。
- 片側検定: グループ1の分布がグループ2よりも大きい（または小さい）。
たとえば、以下の状況を考えます：
- 例: 新薬Aと従来薬Bの血圧への効果を比較する場合。
- H0: 新薬Aと従来薬Bは血圧に与える効果が同じである。
- H1: 新薬Aのほうが従来薬Bよりも効果が高い（片側検定の場合）。
仮説設定で注意すべきポイント
- 方向性を明確にする
- 実験や調査の目的に応じて、両側検定または片側検定を選びます。片側検定の場合、結果の方向をあらかじめ想定する必要があります。
- 検定力の確保
- サンプルサイズが小さい場合、帰無仮説を棄却するのに十分な統計的証拠が得られないことがあります。そのため、検定力（Type II エラーを減らす能力）を意識する必要があります。
実際の例で考えてみよう！
シチュエーション: 新薬Aと従来薬Bの比較
新薬A（グループ1）と従来薬B（グループ2）の効果を調べるために、以下のデータを収集しました：
- グループ1（新薬A）: [12, 15, 20, 18]
- グループ2（従来薬B）: [10, 14, 17, 19]
手順:
- データを結合して順位付け
- データ全体: [10, 12, 14, 15, 17, 18, 19, 20]
- 順位: [1, 2, 3, 4, 5, 6, 7, 8]
- グループ1（新薬A）: [2, 4, 8, 6]（合計 R1=20）
- グループ2（従来薬B）: [1, 3, 5, 7]（合計 R2=16）
- U統計量を計算
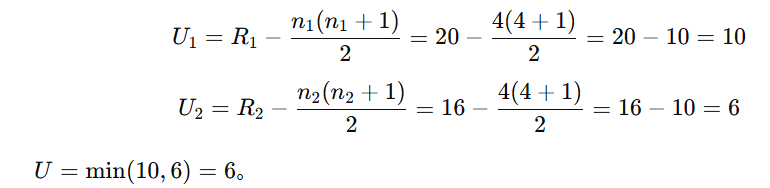
- 有意性の判断
U値を検定表と比較し、帰無仮説を棄却するかを決定します。
マンホイットニーのU検定の限界
マンホイットニーのU検定は多用途で便利な方法ですが、いくつかの限界があります。以下ではその詳細と注意点を解説します：
1. グループ間の分布形状の違いに弱い
マンホイットニーのU検定は、2つのグループの中央値が異なるかどうかを検出するために使われます。しかし、この検定はグループ間の分布形状が大きく異なる場合に影響を受けることがあります。たとえば：
- グループ1が広く分散しているが、グループ2が狭く集中している場合、検定結果が不安定になる可能性があります。
- 実際には分布の形状が異なるだけで中央値は同じ場合でも、検定結果が誤解を招く可能性があります。
2. 大量の順位重複への対応が難しい
データに重複（同順位）が多い場合、順位付けの方法が結果に大きく影響します。特に、連続データではなくカテゴリデータや小数点を持たない整数データの場合、順位の重複が発生しやすくなります。重複データが多いと検定力が低下することがあります。
3. サンプルサイズの制約
マンホイットニーのU検定は小さなサンプルサイズにも適していますが、サンプルサイズが非常に小さい場合、検定表で正確な有意性を判断することが難しくなります。また、大きなサンプルサイズになると検定結果が微小な差にも敏感になるため、実質的な意味が薄い結果を得る可能性があります。
4. データが独立していることが前提
マンホイットニーのU検定では、2つのグループのデータが独立していることが前提です。もしデータがペアになっている場合（例：同一人物の前後データや関連性のある観測データ）、この検定を適用するのは不適切です。その場合、ウィルコクソンの符号付き順位検定を使用するべきです。
5. 効果の大きさを直接測れない
マンホイットニーのU検定は、統計的有意性を評価する方法であり、効果の大きさ（effect size）を直接提供しません。結果が有意であっても、どの程度の差があるのかを理解するには、別途効果量（たとえば、Cliff’s DeltaやRank-Biserial Correlation）を計算する必要があります。
まとめ
仮説設定のポイント:
- 帰無仮説と対立仮説を明確にし、検定の方向性（両側・片側）を選ぶ。
- サンプルサイズやデータの性質に応じて適切な方法を選択する。
限界に注意しながら利用する:
- 分布形状の違いに敏感であることを意識し、データを十分に理解した上で使用する。
- データの重複やサンプルサイズの制約が検定結果に影響する場合があることを認識する。
マンホイットニーのU検定は非常に有用なツールですが、限界を理解した上で正しく使うことが、信頼性の高い分析結果を得るための鍵となります。
