標本平均の標準誤差が小さいということは?
統計学で「標準誤差」とは、ある統計量(例:標本平均)のばらつきを表す指標です。特に標本平均の標準誤差が小さい場合、データにはいくつかの重要な意味があります。この記事では、標準誤差が小さいことの解釈と、それがデータ分析に与える影響についてわかりやすく解説します。
標本平均と標準誤差の基本
標本平均とは?
標本平均は、サンプルデータ(標本)の平均値を指します。母集団の特性を推定するために使用される重要な統計量です。
標準誤差とは?
標準誤差(Standard Error, SE)は、標本平均が母平均からどれだけばらつくかを表します。具体的には、次の式で計算されます:
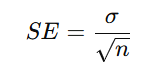
- σ: 母標準偏差(または標本標準偏差)
- n: 標本サイズ
標準誤差が小さいことの意味
- 標本平均が母平均に近い可能性が高い
標準誤差が小さい場合、標本平均が母集団の真の平均値(母平均)を正確に表している可能性が高いです。これにより、推定値の信頼性が向上します。 - データのばらつきが少ない
標準誤差が小さい背景には、元のデータの標準偏差(σ)が小さいことが考えられます。データのばらつきが少ない場合、全体の傾向が安定していると判断できます。 - 標本サイズが大きい
標本サイズ n が増加すると、標準誤差は小さくなります。大きな標本サイズは、母集団の性質をより正確に反映する結果をもたらします。
標準誤差が小さい場合の応用例
1. マーケティングのA/Bテスト
Web広告のクリック率を比較するA/Bテストでは、標本平均の標準誤差が小さいほど、各グループのクリック率の違いを確実に判断できます。例えば、A/B両グループで数千人以上のデータを収集することで、結果の信頼性が高まります。
2. 医薬品の臨床試験
新薬の効果を調べる臨床試験でも、標本平均の標準誤差が小さい場合、薬の効果が本物である可能性が高いと考えられます。特にサンプルサイズを大きくすることで、誤差を減らすことが重要です。
3. 経済データの分析
消費者の平均支出額などを調査する際、標準誤差が小さいと、平均値が経済全体を正確に反映しているといえます。
標準誤差が大きいときの注意点
標準誤差が大きい場合、以下の問題が発生する可能性があります:
- 標本平均が母平均を正確に反映していない。
- 結果の信頼性が低く、結論に不確実性が伴う。
- 標本サイズが不足している可能性がある。
このような場合は、より多くのデータを収集するか、測定精度を向上させることが推奨されます。
まとめ
標本平均の標準誤差が小さいということは、データのばらつきが少なく、標本サイズが十分であることを示しています。このようなデータでは、母集団の特性をより正確に推定できるため、分析の信頼性が向上します。一方で、標準誤差が大きい場合は、追加のデータ収集や分析手法の見直しが必要です。
データ分析の基礎を理解し、適切な結論を導き出すためにも、標準誤差の概念をしっかりと押さえておきましょう!