重相関係数(Multiple Correlation Coefficient)は、複数の説明変数と目的変数との関係を数値で表す統計指標です。特に回帰分析や多変量解析において、モデル全体の適合度を評価する際に使われます。本記事では、重相関係数の定義や計算方法、実用例について詳しく解説します。
重相関係数とは?
重相関係数 R は、複数の説明変数(独立変数)と1つの目的変数(従属変数)の間の相関を表す値で、回帰モデル全体の予測力を示します。その値は 0 から 1 の範囲を取り、以下のように解釈されます:
- R=1:目的変数が説明変数によって完全に説明される。
- R=0:目的変数が説明変数と全く関係ない。
重相関係数は単一の説明変数と目的変数の関係を示す相関係数の拡張版で、複数の説明変数を扱う際に利用されます。
重相関係数の計算方法
重相関係数 R は、以下の数式で定義されます:
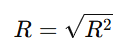
ここで、R2 は 決定係数 を指し、以下の式で求められます:

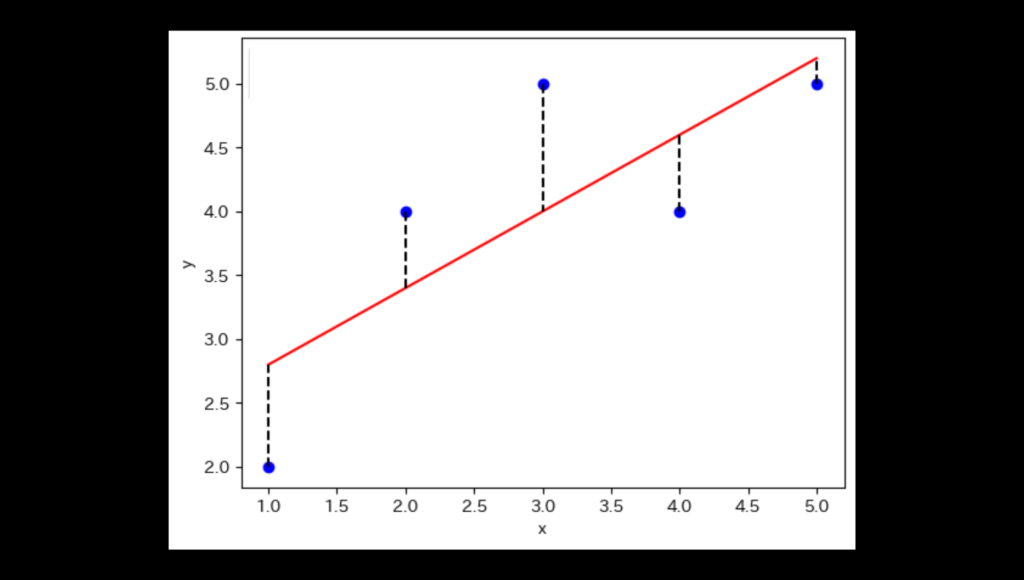
- RSS(Residual Sum of Squares):モデルが説明できなかったデータの変動量。
- TSS(Total Sum of Squares):データ全体の変動量。
この計算式からわかるように、重相関係数はモデルの適合度を測る指標として機能します。
実用例
1. マーケティング分析
複数の広告キャンペーン(説明変数)が売上(目的変数)にどれほど影響しているかを評価する際に、重相関係数を用います。
具体例
- X1:テレビ広告費
- X2:SNS広告費
- X3:検索広告費
- Y:売上
重相関係数 RRR を計算することで、これら3つの広告施策が売上をどれだけ説明できるかを測定します。
2. 教育データの分析
学生の成績(目的変数)に対して、勉強時間、授業の出席率、家庭環境(説明変数)がどの程度影響しているかを調べる際にも使われます。
具体例
- X1:勉強時間
- X2:出席率
- X3:親の教育レベル
- Y:試験成績
重相関係数を使うことで、これら要因の総合的な影響力を評価できます。
重相関係数の活用場面
- モデル全体の適合度評価
回帰分析において、重相関係数はモデルがどの程度データを説明できるかを測定します。高い重相関係数はモデルが良く適合していることを意味します。 - 予測力の向上
説明変数を追加することで重相関係数が上昇する場合、モデルの予測力が向上していると判断できます。ただし、過剰適合(オーバーフィッティング)を避けるため注意が必要です。 - 変数選択の指針
重相関係数の変化を観察することで、モデルに含めるべき変数を選択する際の指針となります。
重相関係数と関連指標
1. 決定係数 (R2)
重相関係数は決定係数の平方根です。R2 はモデルの説明力を直接的に表すため、重相関係数と併せて確認します。
2. 調整済み決定係数
説明変数の数が多くなると、決定係数や重相関係数が過大評価される可能性があります。調整済み決定係数を用いることで、この問題を緩和できます。
重相関係数の限界
- 因果関係を示さない
重相関係数はあくまで相関を測定する指標であり、因果関係を直接示すものではありません。 - 多重共線性の影響
説明変数間に高い相関(多重共線性)がある場合、重相関係数の解釈が困難になることがあります。 - 非線形関係への対応
重相関係数は線形モデルに基づいているため、非線形な関係には対応できません。
まとめ
重相関係数は、複数の説明変数と目的変数の間の関係を評価する上で非常に便利な指標です。マーケティング、教育、医療など、さまざまな分野で活用され、回帰モデル全体の適合度を確認するのに役立ちます。ただし、その限界を理解し、他の指標と組み合わせて適切に活用することが重要です。
この記事を参考に、重相関係数を活用してデータ分析のスキルをさらに向上させてください!