データ分析や回帰分析を行う際に重要な概念の一つとして「異方分散性(heteroscedasticity)」があります。本記事では、異方分散性の基本的な定義から、どのように検出し、対処するのかについてわかりやすく解説します。
異方分散性とは?
異方分散性とは、データの誤差項(残差)の分散が一定でない性質を指します。回帰分析では通常、誤差項の分散が一定(等分散性)であることが前提とされていますが、この前提が満たされない場合、異方分散性が生じていると言います。
異方分散性の例
例えば、次のようなデータを考えてみましょう。
- 低所得者層では支出のばらつきが少ないが、高所得者層になるにつれて支出のばらつきが大きくなる。
この場合、支出の分散が所得によって変化しており、異方分散性が存在します。
等分散性が求められる理由
等分散性は、次の理由から重要です:
- 回帰係数の推定値が不偏で効率的である。
- 検定結果(p値や信頼区間)が信頼できる。
異方分散性がある場合、これらの性質が崩れ、モデルの信頼性が低下します。
異方分散性の検出方法
異方分散性を検出するための代表的な手法をいくつか紹介します。
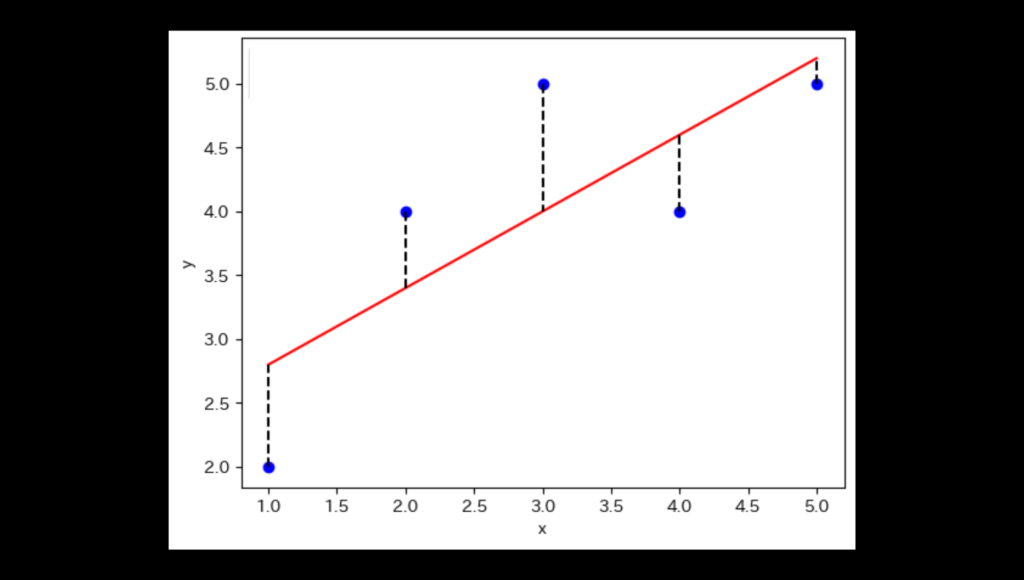
1. 視覚的検出
残差プロットを作成し、独立変数に対する残差の分布を確認します。異方分散性がある場合、以下のようなパターンが見られます:
- 漏斗状(狭くなったり広がったりしている)。
- 系統的な広がり方。
2. Breusch-Pagan検定
Breusch-Pagan検定は、異方分散性を統計的に検出する手法の一つです。帰無仮説は「等分散性がある」であり、p値が有意水準を下回れば異方分散性があると判断します。
3. White検定
White検定は、モデルに特定の形式を仮定しない方法です。非線形な異方分散性にも対応可能で、頑健な手法とされています。
異方分散性への対処法
異方分散性が検出された場合の主な対処法を以下に示します。
1. 変数の変換
従属変数または独立変数を変換することで異方分散性を軽減できます。
- 対数変換(log変換)
- 平方根変換
2. 頑健標準誤差の利用
通常の標準誤差の代わりに、**頑健標準誤差(robust standard errors)**を使用することで、異方分散性がモデルに与える影響を軽減できます。
3. 重み付き最小二乗法(WLS: Weighted Least Squares)
異方分散性が発生している部分に応じて重みを付けることで、等分散性に近づける方法です。分散が大きいデータポイントの影響を調整できます。
異方分散性が分析に及ぼす影響
異方分散性を放置すると、次のような問題が生じる可能性があります:
- 回帰係数の推定値は依然として不偏ですが、効率性が低下します。
- 検定の信頼性が損なわれる。
- モデルの予測精度が低下する。
そのため、異方分散性が検出された場合は適切な対処が必要です。
まとめ
異方分散性は、データ分析においてしばしば発生する問題ですが、適切な検出と対処を行うことで、その影響を最小限に抑えることができます。Breusch-Pagan検定やWhite検定などを活用して異方分散性を検出し、頑健標準誤差や変数変換などの手法を組み合わせることがポイントです。
データの特性に応じた適切な手法を選択し、信頼性の高い分析を心がけましょう!
データ分析のキャリアを目指すあなたへ!
統計学や機械学習は、データサイエンスやAIエンジニアリングの基盤となる分野です。
こうした知識を深め、実践的なスキルを身につければ、需要の高いAI関連職種でのキャリア形成も目指せます。
未経験からでも安心して学べるおすすめのキャリア支援サービスについて、こちらの記事で詳しく解説していますので、ぜひチェックしてみてください。