ベルヌーイ試行とは？確率論の基礎を理解しよう

導入

確率論や統計学で頻繁に登場する「ベルヌーイ試行」は、非常にシンプルながらも強力な概念です。この試行は、様々な確率モデルの基礎となるものです。本記事では、ベルヌーイ試行の基本的な概念、数式、そしてその応用例について解説します。

ベルヌーイ試行（Bernoulli trial）とは、二つの可能な結果を持つ試行のことを指します。一般的には「成功」または「失敗」という二項に分類され、例えばコインの裏表、サイコロで特定の目が出るかどうか、などが例として挙げられます。

ベルヌーイ試行の結果は、ベルヌーイ分布に従います。成功の確率を ppp、失敗の確率を 1−p1-p1−p とすると、確率質量関数（PMF）は以下のように表されます。

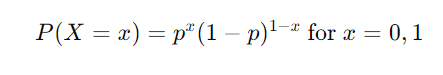
ここで、x=1 は成功、x=0 は失敗を示します。

ベルヌーイ試行は、バイナリデータのモデリングや、繰り返し行われる試行の確率を評価する際に頻繁に用いられます。例えば、以下のようなケースで応用されます。

ベルヌーイ試行が独立に繰り返されるとき、その結果は二項分布に従います。例えば、10回コインを投げたときに「表」が出る回数を考える場合、これはベルヌーイ試行を10回繰り返したものであり、二項分布でモデル化されます。

ベルヌーイ試行は、確率論や統計学の基礎中の基礎です。このシンプルな試行が、多くの複雑な確率モデルの基盤となります。特に、成功と失敗という二項対立を扱う際に、その理解が非常に重要になります。