統計的検定では、データの分布を理解することが重要です。
特に、二項分布と正規分布は、多くの統計手法で用いられます。本記事では、それぞれの分布のグラフ形状の違いと関係性について解説します。
二項分布のグラフ形状
二項分布は、試行回数n と成功確率 pによって決まる離散型確率分布です。
例えば、コイン投げをn 回行い、表が出る回数を数える場合、二項分布に従います。
二項分布の特徴
二項分布のグラフ形状は以下の特徴を持ちます:
- nが小さい場合、分布は非対称になりやすい。
- pが 0.5 に近いほど左右対称に近づく。
- nが大きくなると、分布は正規分布に近づく(中心極限定理)。
例えば、 n=10,p=0.5の場合、二項分布のグラフは左右対称に近いベル型になりますが、 p=0.2やp=0.8 の場合は非対称な形になります。
正規分布のグラフ形状
正規分布は、連続型確率分布であり、平均μ と標準偏差σ によって決まります。一般に、以下の特徴を持ちます。
正規分布の特徴
- 平均値 μ を中心に左右対称。
- 確率密度関数は釣鐘型(ベルカーブ)。
- 中心付近にデータが集中し、端に行くほど確率が低くなる。
例えば、二項分布の試行回数n を増やすと、正規分布に近づきます。これは中心極限定理により説明できます。
二項分布と正規分布の関係
二項分布は、試行回数が多いと正規分布に近づく性質を持っています。具体的には、 nが大きい場合、以下の正規近似が可能です:
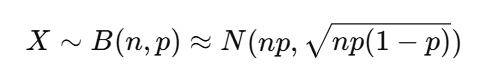
正規近似の条件
この近似が成り立つ条件は、 npおよびn(1-p) の両方が十分に大きいことです(一般に 5 以上が目安)。
まとめ
- 二項分布 は離散型で、試行回数 nと成功確率p に依存。
- 正規分布 は連続型で、平均 μと標準偏差σ による釣鐘型の形状。
- 二項分布は が増えると正規分布に近づく(中心極限定理)。
統計的検定では、この関係を利用して二項分布の確率を正規分布で近似し、計算を簡略化することができます。