統計検定3級範囲　『箱ひげ図』の解説

箱ひげ図とは？

箱ひげ図は、データセットの中心的な傾向や分布の広がりを視覚的に表現する手法です。このグラフは、データの最小値、最大値、四分位範囲（IQR）、および中央値を示すことで、データのばらつきや外れ値を簡単に把握することができます。

箱ひげ図の構成要素

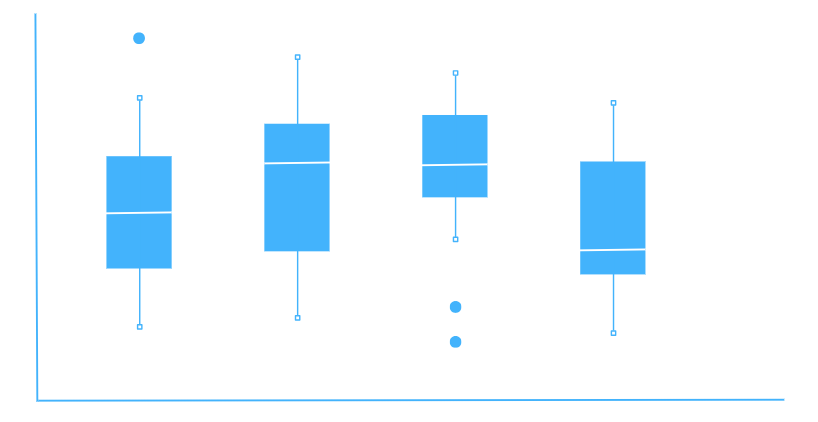
上記のグラフを用いて説明していきます。

箱（ボックス）

箱の下端は第1四分位数（Q1）を、上端は第3四分位数（Q3）を示します。箱の範囲は四分位範囲（IQR）を表し、データの中心50%がこの範囲に含まれます。

中央値

箱の中に引かれている白い線はデータの中央値（第2四分位数、Q2）を示します。中央値はデータセットを上下に分割する点であり、データの中心傾向を表します。

ひげ

箱から伸びる縦線は「ひげ」と呼ばれ、データの最小値と最大値を示します。ただし、ひげの範囲は通常、Q1からQ3までの範囲を1.5倍した範囲内のデータを表します。この範囲を超えるデータ点は外れ値として扱われます。

外れ値

ひげの範囲外にあるデータ点は外れ値としてプロットされ、個別の点で表されます。外れ値は異常値や特異な観測値を示すため、分析の際には特に注目されます。

箱ひげ図の読み方

箱ひげ図を読む際には、以下のポイントに注目します。

箱の位置

箱がグラフのどの位置にあるかでデータの偏りを確認します。箱がグラフの下部にある場合、データは下に偏っており、上部にある場合は上に偏っています。

箱の広さ

箱が広いほど、データのばらつきが大きいことを示します。逆に、箱が狭い場合、データが集中していることを意味します。

ひげの長さ

ひげが長いほど、データの範囲が広いことを示します。ひげの長さに違いがある場合、データの分布に偏りがある可能性があります。

外れ値

外れ値が多い場合、データセットに異常値が含まれている可能性があります。

箱ひげ図の実例

実際に箱ひげ図を用いたデータの分析例を見てみましょう。以下は、あるクラスのテストの点数分布を箱ひげ図で表したものです。

• 中央値が高い：クラス全体の学力は高い傾向にあります。
• 外れ値が1つある：一部の生徒が極端に低い点数を取っている可能性があります。
• 箱が狭い：多くの生徒が似たような点数を取っていることを示しています。

Appendix：箱ひげ図の作成方法

箱ひげ図は、手動でも作成可能ですが、ExcelやPythonなどのツールを使用することで簡単に作成できます。以下に、Pythonを用いた基本的な箱ひげ図の作成方法を紹介します。

是非Google Colaboratoryなどで試してみてください。

import matplotlib.pyplot as plt

# サンプルデータdata = [70, 85, 90, 60, 78, 88, 92, 55, 80, 76]# 箱ひげ図の作成plt.boxplot(data)
plt.title("Box Plot of Test Scores")
plt.ylabel("Score")
plt.show()

このコードは、テストの点数分布を視覚化するシンプルな箱ひげ図を作成します。

まとめ

箱ひげ図は、データセットの概要を直感的に把握するための強力なツールです。統計検定3級では、箱ひげ図を用いてデータの特徴を読み取り、適切な分析を行うことが求められます。この記事を参考にして、箱ひげ図の理解を深め、試験に備えてください。

統計検定3級の練習問題

統計検定3級の練習問題にチャレンジできるアプリケーションを作りました！

下記リンクから是非トライしてみてください！

【一問一答形式】統計検定3級を受験する方へ！　無料の練習問題アプリ 問1~10

参考書の案内

統計学の基礎をしっかりと身につけたい方や、統計検定の合格を目指している方におすすめの問題集です。この書籍は、統計学の理論をわかりやすく解説しており、実際の試験に近い問題を多数収録しています。問題を解くことで、統計に関する知識を実践的に深めることができます。

自信を持って試験に臨むために、ぜひ手に取ってみてください。

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］ [ 日本統計学会 ] 価格：2,200円（税込、送料無料) (2024/8/19時点)

日本統計学会公式認定　統計検定　3級・4級　公式問題集［CBT対応版］ [ 日本統計学会 ] 価格：2,200円（税込、送料無料) (2024/8/19時点)