カイ二乗検定とは？データ分析での活用法を解説！

By /

はじめに

統計学の世界には、多くの検定手法が存在しますが、その中でもよく使われるのが「カイ二乗検定」です。この検定は、カテゴリーデータ（質的データ）を扱う際に、観測データが期待値とどれだけ異なるかを評価するために使用されます。本記事では、カイ二乗検定の基本的な概念から、実際の活用方法までをわかりやすく解説します。

カイ二乗検定とは？

カイ二乗検定は、観測されたデータと期待されるデータ（理論的に予測されるデータ）の違いが統計的に有意であるかを判断するための検定手法です。これにより、例えば、アンケート結果が理論上の期待値と一致しているかどうかを確認することができます。

カイ二乗検定の種類

カイ二乗検定には主に次の2種類があります。

適合度検定

あるカテゴリのデータが、特定の理論分布（例：正規分布、ポアソン分布）に適合しているかどうかを検定します。

独立性の検定

2つのカテゴリ変数が独立しているかどうかを検定します。例えば、性別と購買行動が関連しているかどうかを確認する際に使われます。

カイ二乗検定の手順

カイ二乗検定の一般的な手順は以下の通りです。

仮説設定

  • 帰無仮説 (H0​)：「観測データは期待値と一致している」
  • 対立仮説 (H1)：「観測データは期待値と一致していない」

期待値の計算

  • 各カテゴリの期待される頻度を計算します。例えば、コインの裏表が均等に出るなら、100回の投げで50回ずつになることが期待されます。

カイ二乗値の計算

  • 以下の式を使って、観測値と期待値の差を計算します。

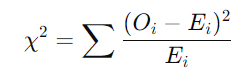
ここで、Oi​は観測値、Ei​は期待値です。

自由度と有意水準の設定

自由度を求め、有意水準（通常5%）と照らし合わせます。

カイ二乗分布表で結果を判定

計算したカイ二乗値を基に、カイ二乗分布表を使って、帰無仮説を棄却するかどうかを判断します。

カイ二乗検定の実例

例: 商品の売れ筋分析

ある店舗で新商品AとBが販売されました。100名に選んでもらったところ、商品Aを選んだのが60名、商品Bを選んだのが40名でした。この結果が、商品AとBが同等に好まれるという仮説と一致しているかをカイ二乗検定で確認できます。

実際に解いてみましょう。

仮説設定

  • 帰無仮説 (H0): 商品Aと商品Bが同等に好まれる（すなわち、AとBが選ばれる確率は50:50である）。
  • 対立仮説 (H1): 商品Aと商品Bは同等には好まれていない（選ばれる確率が異なる）。

期待値の計算

帰無仮説が正しい場合、商品Aと商品Bが選ばれる人数はそれぞれ50人であるはずです（100人中50%がA、50%がBを選ぶ）。

カイ二乗統計量の計算

カイ二乗統計量は以下の式で計算されます。

具体的に計算すると:

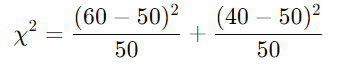
  • 商品A: 観測値 = 60, 期待値 = 50
  • 商品B: 観測値 = 40, 期待値 = 50

カイ二乗統計量は χ2=4.0 となりました。

次に、このカイ二乗統計量に対応するp値を計算し、帰無仮説を棄却するかどうかを判断します。この場合、自由度は df=1 です。

p値を計算して、結果を確認し得られたp値は約0.0455です。

一般的に、p値が0.05未満であれば帰無仮説を棄却します。したがって、この結果は商品Aと商品Bが同等に好まれるという仮説（帰無仮説）を棄却し、AとBの間に好まれる度合いに有意な差があると結論付けることができます。

カイ二乗検定の限界

カイ二乗検定は非常に有用ですが、いくつかの注意点もあります。特に、期待値が極端に小さい場合、検定結果が不安定になることがあります。このような場合は、フィッシャーの正確検定など、他の手法を考慮する必要があります。

まとめ

カイ二乗検定は、データ分析においてカテゴリーデータを扱う際に強力なツールとなります。本記事では、カイ二乗検定の基礎から実際の応用までを解説しましたが、実際にデータを扱う際には、適切な仮説設定と手順を踏んで検定を行うことが重要です。統計的な手法を駆使して、より深いデータ分析を目指しましょう！

参考書の案内

統計学の基礎をしっかりと身につけたい方や、統計検定の合格を目指している方におすすめの問題集です。この書籍は、統計学の理論をわかりやすく解説しており、実際の試験に近い問題を多数収録しています。問題を解くことで、統計に関する知識を実践的に深めることができます。

自信を持って試験に臨むために、ぜひ手に取ってみてください。



関連投稿

コメントする

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

上部へスクロール