統計学では、限られたデータ(サンプル)を用いて母集団の特性を推定することが重要です。特に、母集団の平均(μ–)をできるだけ正確に推定するためには、適切な方法を選択する必要があります。本記事では、そのための代表的な手法を解説します。
1. サンプル平均の利用
母集団の平均を推定する基本的な方法は、サンプル平均(x–)を計算することです。サンプル平均は以下の式で求められます。
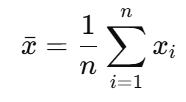
ここで、xi はサンプルの各データ、n はサンプルの大きさです。サンプルが十分に大きければ、x– は母平均μに近い値を示します。
2. 中心極限定理を利用する
中心極限定理によれば、サンプルサイズ が十分に大きい場合、サンプル平均 は正規分布に近づきます。つまり、
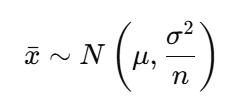
ここで、σ2 は母集団の分散です。これにより、サンプル平均を用いた推定が理論的に正当化されます。
3. 信頼区間を用いた推定
点推定(単一の値としての推定)だけではなく、信頼区間(confidence interval) を用いることで、推定の信頼性を向上できます。
母集団の分散が既知の場合、信頼区間は次のように表されます。
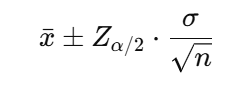
ここで、
- Zα/2は標準正規分布における上側 α/2の百分位点
- σは母集団の標準偏差。
母集団の分散が未知の場合は、t分布 を利用します。
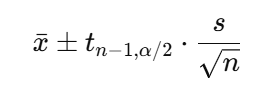
4. 標本サイズの重要性
母平均を高い信頼性で推定するためには、十分なサンプルサイズ を確保することが重要です。
サンプルサイズ nを決定するための一般的な式は以下の通りです。
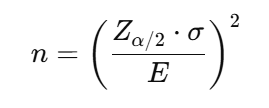
ここで、 Eは許容誤差(margin of error)を表します。サンプルサイズが大きいほど、推定の精度が向上します。
5. 無作為抽出の重要性
推定の精度を向上させるためには、ランダムサンプリング(無作為抽出) を行うことが不可欠です。偏りのあるサンプリングでは、母平均の推定値が不正確になる可能性があります。
例えば、
- 単純無作為抽出(SRS: Simple Random Sampling)
- 層別抽出(Stratified Sampling)
- 系統抽出(Systematic Sampling)
などの手法を適切に活用することで、代表性のあるデータを取得できます。
まとめ
母集団の平均を信頼性高く推定するためには、以下の点が重要です。
- サンプル平均を利用する:サンプル平均は母平均の良い推定量となる。
- 中心極限定理を活用する:サンプルサイズが十分ならば正規分布に従う。
- 信頼区間を求める:点推定だけでなく信頼区間を考慮する。
- 適切なサンプルサイズを確保する:誤差を小さくするには十分なサンプル数が必要。
- 無作為抽出を行う:サンプリング方法を適切に選択し、偏りをなくす。
これらを意識することで、統計的に信頼性の高い推定が可能になります。