相関係数(correlation coefficient)は、2つの変数の関係の強さと方向を示す指標です。特に、最も一般的に使われるピアソンの相関係数(Pearson’s correlation coefficient)は、-1 から 1 の範囲を取り、以下のような意味を持ちます。
- 1:完全な正の相関(片方が増えるともう片方も増える)
- 0:相関なし(変数間に線形関係がない)
- -1:完全な負の相関(片方が増えるともう片方が減る)
ピアソンの相関係数の計算式
ピアソンの相関係数 rは、以下の式で計算されます。
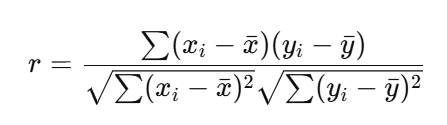
ここで:
- xiおよび は、yiそれぞれの変数のデータ点
- x–およびy– は、それぞれの変数の平均値
この式は、共分散を標準偏差で割ったものと考えることもできます。
相関係数の解釈
相関係数の値によって、以下のように解釈されます。
| 相関係数 | 関係の強さ |
|---|---|
| 0.7 ~ 1.0 | 強い正の相関 |
| 0.3 ~ 0.7 | 中程度の正の相関 |
| 0.0 ~ 0.3 | 弱い正の相関 |
| -0.3 ~ 0.0 | 弱い負の相関 |
| -0.7 ~ -0.3 | 中程度の負の相関 |
| -1.0 ~ -0.7 | 強い負の相関 |
ただし、相関が高いからといって因果関係があるとは限りません。
スピアマンの順位相関係数
ピアソンの相関係数は線形関係を測定しますが、非線形関係がある場合にはスピアマンの順位相関係数(Spearman’s rank correlation coefficient)を使うこともあります。
スピアマンの相関係数 は、各データの順位に対するピアソンの相関係数として計算され、以下の式を用います。
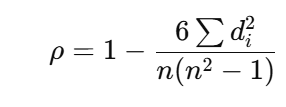
ここで:
- diは対応するデータ点の順位の差
- nはデータ点の数
まとめ
- 相関係数 は2つの変数の関係の強さと方向を示す指標。
- ピアソンの相関係数 は線形関係の強さを測る。
- スピアマンの順位相関係数 は非線形関係にも対応可能。
- 相関が高くても因果関係があるとは限らない ため、解釈には注意が必要。
統計分析を行う際には、適切な相関係数を選択し、データの関係を正しく理解することが重要です。