今回はサンプルサイズの算出で使われる重要な指標の『効果量』について解説します。
ABテストなど施策の効果検証において重要な指標なので是非身に着けて頂ければ幸いです。
効果量とは
まず始めに効果量とは何なのか解説します。
効果量とは統計学において、2つのグループ間の差や関係の大きさを示す指標です。
効果量は、単に統計的に有意であるかどうかを判断するだけでなく、その差が実際にどれほどの影響を持つのかを理解するのに役立ちます。
例えば、ある医薬品の臨床試験で、新薬が既存薬よりも効果があるかどうかを検討しているとします。 試験の結果、新薬の効果が既存薬よりもわずかに高いとします。p値が0.05未満であれば、統計的に有意と見なされます。
しかし、効果量 が低ければ(=関係性が小さければ)、その効果は小さいとされ、実際の臨床での意味合いは乏しいかもしれません。逆に、効果量が大きければ、効果があるとされ、新薬が臨床現場で推奨される可能性が高まります。
このように、効果量を見ることで、統計的に有意な結果が実際にどれだけ臨床的に有用かを判断できます。
効果量の種類
そんな効果量にもいくつか種類があります。
平均の差の効果量 (Cohen’s d)
2つのグループの平均の差を、標準偏差で割ったものです。標準偏差を基準にしているため、グループ間の差が標準偏差の何倍に相当するかがわかります。
例: Cohen’s d = 0.2(小さい効果)、0.5(中程度の効果)、0.8(大きい効果)
計算方法
Cohen’s d は、下記の式で計算されます。
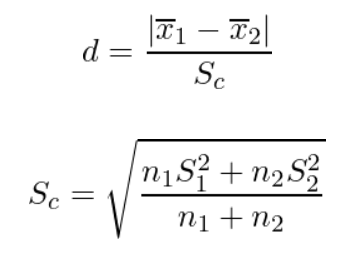
x:標本平均 S2:標本分散 n:サンプルサイズ
使い分け
Cohen’s d は主に、2つのグループ間の平均の差の大きさを比較するときに使用されます。教育、心理学、医療の分野で広く使われています。
実例
ある学校で新しい教育プログラムが導入され、その効果を評価するために2つのクラス(新プログラムを受けたクラスと従来のプログラムを受けたクラス)の成績平均を比較したとします。
- 新プログラムクラス
- 平均成績: 85点
- 生徒数:20人
- 分散:5
- 従来プログラムクラス
- 平均成績: 80点
- 生徒数:25人
- 分散:8
この場合、Cohen’s d を計算すると、Cohen’s d = 1.936491673 となります。これにより新プログラムは大きな効果を示し、新しいプログラムが従来のプログラムよりも効果的であることがわかります。
相関係数 (r)
2つの変数間の関係の強さを示す効果量です。相関係数は -1から1までの値を取り、0に近いほど関連が弱いことを示します。
計算方法
Pearsonの相関係数 r は、2つの変数間の線形関係の強さを示す指標で、以下の式で計算されます。
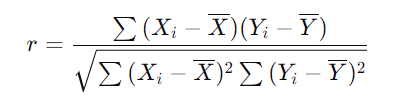
使い分け
Pearsonの相関係数は、2つの連続変数の間の関係を評価するときに使われます。心理学や社会科学、自然科学の分野で、変数間の関連性を調べる際によく使用されます。
実例
ある研究で、学生の勉強時間と成績の関係を調べたとします。勉強時間が増えるにつれて成績が向上するかを確認するために、Pearsonの相関係数を計算します。例えば、相関係数が r=0.6だった場合、これは中程度から強い正の相関を示し、勉強時間が増えると成績が良くなる傾向があることを意味します。
決定係数 (R²)
回帰分析で用いられ、独立変数が従属変数の変動をどの程度説明できるかを示す指標です。0から1までの値を取り、1に近いほどモデルの説明力が高いことを示します。
計算方法
決定係数 R² は、回帰分析でモデルがどれだけデータを説明しているかを示す指標で、以下の式で計算されます。

使い分け
R² は、回帰モデルが従属変数の変動をどの程度説明できるかを評価するときに使用されます。経済学や自然科学などの分野で、モデルの説明力を評価する際に使われます。
実例
ある経済モデルで、消費支出を予測するために、所得と支出のデータを使った回帰分析を行ったとします。回帰モデルが得られ、R² = 0.85 だった場合、これはモデルが消費支出の85%を説明できることを示し、非常に良好なモデルであると判断できます。
まとめ:効果量の重要性
- 実質的な意義
- 統計的に有意であっても、効果量が小さい場合、その差や関係が実際の場面で意味がないこともあります。効果量が大きければ、統計的に有意でなくても、結果が実質的に重要である可能性があります。
- メタ分析
- 複数の研究結果を統合する際、効果量を使うことで異なる研究間の結果を比較しやすくなります。
効果量は、単に「違いがあるかどうか」だけでなく、「その違いがどれほどのものか」を考える際に不可欠な指標です。





ピンバック: p値だけ見て満足?「効果量」でわかる本当の差 - RWE