期待値は、確率論や統計学で非常に重要な概念の一つです。確率分布に基づくデータの平均的な値を示すもので、現象の長期的な傾向を理解するのに役立ちます。本記事では、期待値の基本的な定義から具体例まで、分かりやすく解説します。
期待値の定義とは?
期待値(英: Expected Value)とは、確率分布における「重み付き平均」のようなもので、次のように計算されます。
離散型確率分布の場合
確率変数 X の期待値 E[X] は次の式で定義されます。
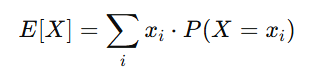
ここで:
- xi:確率変数 X の取りうる値
- P(X=xi): xi が起こる確率
連続型確率分布の場合
確率密度関数 f(x) に基づく期待値は、次のような積分で定義されます。
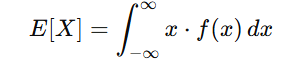
この式では、確率密度関数 f(x)によって、各値 x がどれだけの「重み」を持つかを反映します。
期待値の具体例
1. サイコロの期待値
普通の6面サイコロを振る場合を考えます。このサイコロの目は 1,2,3,4,5,6 で、それぞれの確率は 1/6 です。
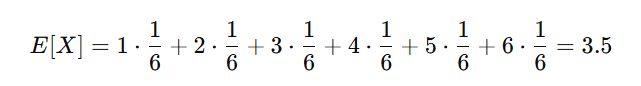
サイコロを無数に振った場合、平均的に出る目は 3.5 になると予測されます。
2. 正規分布の期待値
標準正規分布(平均 0、分散 1)では、期待値はその平均値に一致します。このように、対称な分布では期待値が直感的にその「中心」を表すことが多いです。
期待値の性質
期待値には以下のような便利な性質があります。
- 線形性
期待値は線形性を持ちます。すなわち、確率変数 X,Y とスカラー a,b に対して:
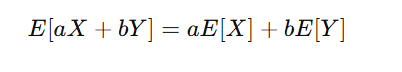
- 加法性
互いに独立な確率変数 X,YX, YX,Y に対して:E[X+Y]=E[X]+E[Y]
期待値の応用
期待値は統計学や意思決定理論など、多くの分野で応用されています。以下はその具体例です。
- ギャンブルや投資
各選択肢の期待値を計算することで、長期的に最も有利な選択肢を判断できます。 - 機械学習
モデルの性能指標(例えば損失関数)の期待値を最小化することが、学習アルゴリズムの目標となります。 - 保険業界
保険料の設定は、損害額の期待値に基づいて計算されます。
まとめ
期待値は確率分布を理解するための基本的な指標であり、現象の「平均的な傾向」を示します。その計算方法はシンプルですが、応用範囲は非常に広く、統計や実務において欠かせない概念です。この記事をきっかけに、期待値についてさらに深く学んでみてください!