はじめに
統計検定準1級で扱われる包除原理は、複数の事象の和の確率を求める際に不可欠です。この原理を理解し適用することで、複雑な確率問題を効率的に解くことが可能となります。
包除原理とは?
包除原理とは、複数の集合が重複する場合に、それらの集合の和(統合された集合)の要素数を正確に計算するための数学的法則です。
具体的には、複数の事象の発生確率を求める際に、単純に各事象の確率を加算するだけではなく、事象間の重複部分を適切に除去する必要があります。
この原理は、集合論において重要な位置を占め、確率論、統計学、データ分析など、多くの分野で応用されています。
包除原理を用いることで、例えば『3つの集合の和集合の要素数を求める場合』、個々の集合の要素数を加算した後、2つずつの集合に共通する要素を減算し、全ての集合に共通する要素を再度加算することで、正確な要素数を計算します。
包除原理の計算方法と公式
基本的な公式は次のとおりです。
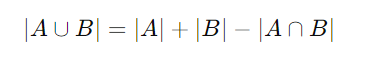
これを三つ以上の集合に拡張すると、次のようになります。
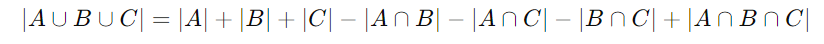
実例での計算
例えば、ある調査で、英語を話せる人、フランス語を話せる人、スペイン語を話せる人がそれぞれ100人、50人、30人おり、これらの言語の組み合わせで重複する人数がある場合の総数を求めます。具体的な重複人数を差し引き、上記の公式を用いて計算します。
実例での包除原理の計算詳解
英語を学んでいる学生が100人、フランス語が50人、スペイン語が30人、英語とフランス語の両方を学んでいる学生が20人、英語とスペイン語の両方を学んでいる学生が10人、フランス語とスペイン語の両方を学んでいる学生が5人、そして全ての言語を学んでいる学生が3人いる場合、少なくとも一つの言語を学んでいる学生の数を計算します。
包除原理により、少なくとも一つの言語を学んでいる学生の総数は次のように計算されます。
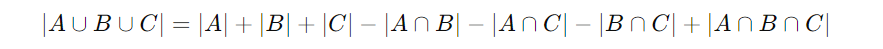
ここで、
- ∣A∣、∣B∣、∣C∣ はそれぞれ英語、フランス語、スペイン語の学生数。
- ∣A ∩ B∣、∣A ∩ C∣、∣B ∩ C∣ は二言語を学んでいる学生数。
- ∣A ∩ B ∩ C∣ は三言語全てを学んでいる学生数。
数値代入
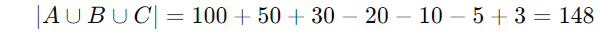
この計算により、少なくとも一つの言語を学んでいる学生は合計148人であることがわかります。
この実例を通じて、包除原理がどのように複数の集合の要素数を効果的に求めるのに役立つかが明確になります。この原理を理解し適用することで、様々な統計的および確率的問題を解決する際に重宝します。
結論
包除原理は、統計検定準1級のみならず、多くの実世界の問題においても役立つ強力なツールです。この原理をマスターすることで、より複雑な確率問題にも自信を持って取り組むことができるようになります。理解と練習を重ね、統計的思考能力を高めましょう。