二項検定を分かりやすく解説！

ある病気に対して医薬品AとBをそれぞれ別の企業が開発しました。

その薬を欲する人にとっては、二つの薬はどちらが効くのか？（優れているのか？）を知りたいと思いますよね。

そういう場合に二項検定を用います。

二項検定の手順を次に記載します。

二項検定の手順

Step.1　帰無仮説（H₀）と対立仮設（H_A）を立てる

　帰無仮説＝比べるものが等しい
　対立仮設＝比べるものが等しくない

Step.2　検定統計量を計算する

薬の有効率（投薬した10人の中で〇人に対して効果があった）

Step.3　帰無分布を作成する

　二項分布の一般式を用いてそれぞれの場合における確率を計算します。
　P(X=x)=_nC_x・p^x・(1-p)^n-x
　　n=データの数、x=どのデータの場合か、p=統計検定量の確率

Step.4　棄却域を設定する

二項分布からの端に設定し、片側か両側を5%もしくは1%の範囲未満に収まるように設定。

Step.5　棄却できるか？を判断する

比べるデータの統計検定量（何人に効果があったのか）が棄却域に入るのか？入らないのか？をチェックします。
入る場合＝帰無仮説（H₀）は棄却されるので「比べるものが等しい」が否定され、2つのデータは異なる（有意差がある（P<0.05））
入らない場合＝帰無仮説（H₀）は棄却されないので「比べるものが等しい」が肯定され、2つのデータは同じ（有意差がない）

検定のStepを学んだところで実践編です。

例題

10人の被験者に対して医薬品A,Bを投薬すると

医薬品Aの有効率＝0.6
医薬品Bの有効率＝0.4

という結果が見られました。
上記における二項検定を行いましょう。
※今回棄却域の確率は両側検定で5%とします

Step1

帰無仮説（H₀）＝医薬品AとBの有効率は同じである

Step2

統計検定量はそれぞれ、A＝0.6、B＝0.4

Step3

一般式（P(X=x)=_nC_x・p^x・(1-p)^n-x）を用いてそれぞれの場合における確率を計算。

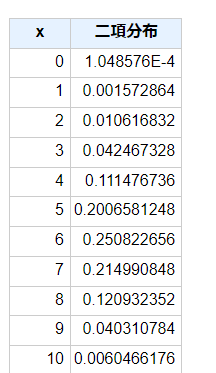
また、二項分布のグラフを作成します。

こちらのサイトをご参考に下さい。

https://keisan.casio.jp/exec/system/1161228844

Step4

棄却域は左右の2.5%(0.025)未満の領域なので、
左はx=0,1,2で右はx=10になります。

Step5

最後に帰無仮説が棄却されるかどうかを見ます。Bの有効率は0.4で有効人数は4人になるため先ほどのグラフでx=4となる部分を見てみましょう。

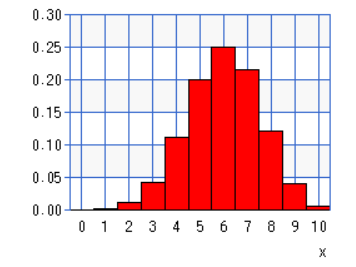
すると、x=4はstep4で設定した棄却域に入っていないため、帰無仮説は棄却されないとなります。

つまり今回の二項検定においては「比べるものが等しい」が肯定され、2つのデータは同じ（有意差がない）という結論になります。

参考書の案内

統計学の基礎をしっかりと身につけたい方や、統計検定の合格を目指している方におすすめの問題集です。この書籍は、統計学の理論をわかりやすく解説しており、実際の試験に近い問題を多数収録しています。問題を解くことで、統計に関する知識を実践的に深めることができます。

自信を持って試験に臨むために、ぜひ手に取ってみてください。

日本統計学会公式認定　統計検定　3級・4級　公式問題集［CBT対応版］ [ 日本統計学会 ] 価格：2,200円（税込、送料無料) (2024/8/19時点)

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］ [ 日本統計学会 ] 価格：2,200円（税込、送料無料) (2024/8/19時点)