マンホイットニーのU検定では『比較するデータに差があると言えるのか？』という問いに答えてくれます。
本記事では、検定の手法から例題までを解説しています。
WMW検定の目的
2つの母集団を想定します。それぞれ母集団Aと母集団Bと名付けておきます。
母集団Aは「何らかの確率分布に従っている」と仮定し、母集団BもAと同じ形状をした何らかの確率分布に従っていると仮定します。
WMW検定ではそれぞれの母集団A、Bから標本を単純無作為に抽出し、それぞれの標本を比較したのち「A,Bの母集団は同じ確率分布に従うか、異なっているか」を判断することが当検定の目的となります。
また、比較時に統計検定量（U）をもって検定を行っていきます。
WMW検定の手順
帰無仮説と対立仮設を立てます。
帰無仮説＝比べるものが等しい
対立仮設＝比べるものが等しくない
Step1.標本サイズと順位和を計算する
それぞれのデータを見て標本サイズを下記のように記載しておきます。
nA=〇 nB=△
A、Bのそれぞれのデータの順位を求め全て足し上げる。
Step2.統計検定量（U）を計算する
Aのグループの統計検定量をU1、BをU２としたとき
U1 = nA・nB＋1/2・nA・(nA＋1) – RA
U2 = nA・nB＋1/2・nB・(nB＋1) – RB
と求めて、より小さい値をUとする
Step3.計算して得たUと臨界値U0.05を比較する
Step2で得たUと、臨界値U0.05を比較します。
臨界値U0.05とは下記の図で得られる値のことで、例えばデータ数がAが4つ、Bが4つの場合は下記のグラフで指し示すとU0.05=0になります。
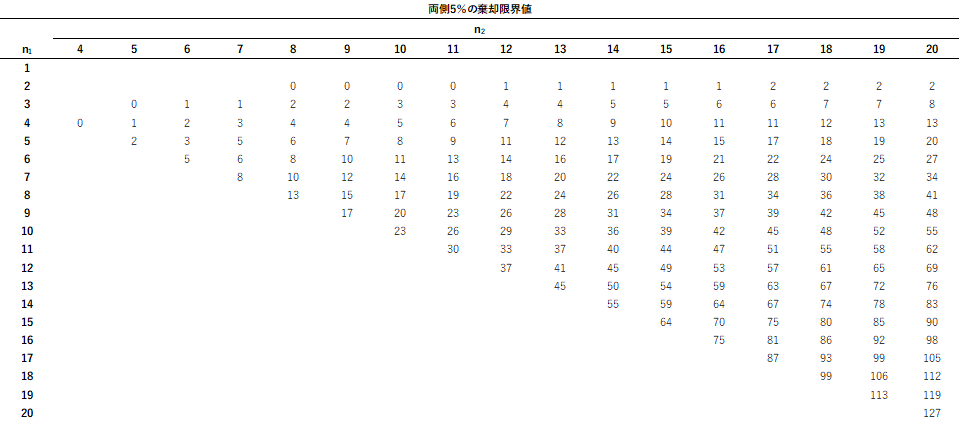
上の表で得た臨界値U0.05とStep2で得たUを比較し
U < U0.05 の場合は「統計的に優位な差が認められた」
U > U0.05 の場合は統計的に優位な差は認められなかった」
結論付けます。
例題
ある学校において男女それぞれ6人の身長に関するデータを得ました。
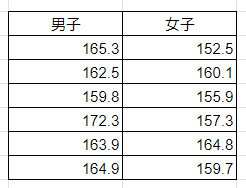
この男女それぞれの身長のデータに差があると言えるのか、検定を行っていきます。
・Step1.標本サイズと順位和を計算する
こちらのサイト使うと計算が楽なので活用していきます。
標本サイズはそれぞれ6人ずつなので、
nA=6 nB=6 となり、サンプルサイズに入力します。
そしてそれぞれのサンプルデータを入力します。
すると結果は下記のようになります。
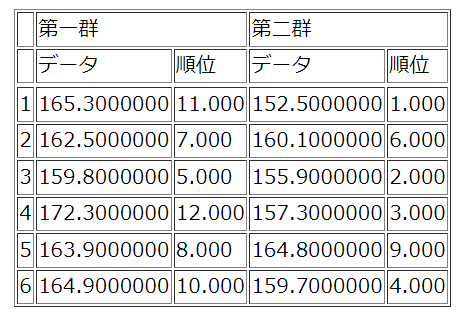
実は添付画像の下に答えが出てしまっているのですが、
一旦はstep通りに例題を解いていきます。
・Step2.統計検定量（U）を計算する
出てきた数字を整理します。
nA=6 nB=6
RA=11+7+5+12+8+10=53
RB=1+6+2+3+9+4=25
これらを下の数式に代入します。
U1 = nA・nB＋1/2・nA・(nA＋1) – RA
U2 = nA・nB＋1/2・nB・(nB＋1) – RB
すると、
U1 = nA・nB＋1/2・nA・(nA＋1) – RA=4
U2 = nA・nB＋1/2・nB・(nB＋1) – RB=32
となり、より小さいほうをUとして採用するので、U=4となります。
Step3.計算して得たUと臨界値U0.05を比較する
Step2で得たUと、臨界値U0.05を比較します。
nA=6 nB=6のため、今回の臨界値U0.05は5となります。
Step2で得たように、U=4なので
U < U0.05 となり「統計的に優位な差が認められた」が結論になります。
