統計分析をする上で、「データが正規分布していいけれど、グループ間の差を比較したい」といった場面に出くわすことがあります。そんなときに役立つのがKruskal-Wallis検定です。本記事では、この検定の基本的な考え方、適用条件、実際の使い方について解説します。
目次
Kruskal-Wallis検定とは?
Kruskal-Wallis検定は、ノンパラメトリック検定の一種で、3つ以上の独立したグループ間で、母集団の中央値に差があるかを検証する方法です。この検定は、正規性や等分散性の仮定が満たされない場合でも利用できるため、実務で非常に役立ちます。
一元配置分散分析 (ANOVA) のノンパラメトリック版と考えることができ、分散分析の代わりに使われることが多いです。
Kruskal-Wallis検定を使うべき場面
以下の条件に当てはまる場合にKruskal-Wallis検定を用いると適切です:
- 独立した3つ以上のグループが存在する。
- 測定変数が順序尺度または間隔尺度・比尺度だが、正規分布を仮定できない。
- グループ内のデータは互いに独立している。
検定の仮説
- 帰無仮説 (H₀): すべてのグループの中央値は等しい。
- 対立仮説 (H₁): 少なくとも1つのグループの中央値が異なる。
検定の手順
- データを順位化する
全データを一つにまとめ、値の小さい順に順位を付けます。値が同じ場合は、順位の平均を取ります。 - 各グループの順位の合計を求める
各グループ内で順位の合計 Ri を計算します。 - 検定統計量を計算する
検定統計量 H は次の式で計算されます:
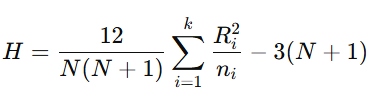
- ここで:
- N: 全サンプル数
- k: グループ数
- ni: グループ i のサンプルサイズ
- Ri: グループ i の順位の合計
- カイ二乗分布を用いて検定
H は自由度 k−1 のカイ二乗分布に従うと仮定します。これに基づき、帰無仮説を棄却するかどうかを判断します。
Kruskal-Wallis検定の利点と限界
利点
- 正規分布や等分散性を仮定しなくてよい。
- 小さいサンプルサイズでも使用可能。
- 順序データでも使える。
限界
- 帰無仮説が棄却された場合、どのグループ間に差があるのかは分からない。そのため、必要に応じて多重比較検定を追加で行う必要があります(例: Dunn検定)。
RやPythonでの実施例
Rの場合
# データ準備
data <- data.frame(
group = factor(c("A", "A", "B", "B", "C", "C")),
value = c(5, 6, 7, 8, 9, 10)
)
# Kruskal-Wallis検定
kruskal.test(value ~ group, data = data)
Pythonの場合
import scipy.stats as stats
# データ準備
group1 = [5, 6]
group2 = [7, 8]
group3 = [9, 10]
# Kruskal-Wallis検定
stats.kruskal(group1, group2, group3)
実際の応用例
応用例 1: 教育プログラムの効果測定
背景
ある学校で、異なる3つの教育プログラム(A, B, C)が提供されました。研究者は、これらのプログラムが学生の学力向上に与える効果を比較したいと考えています。ただし、学力を示すテストスコアが正規分布していないことが確認されています。
データの設定
- グループ A: プログラム A を受けた学生のテストスコア (例: [75, 80, 85, 90])
- グループ B: プログラム B を受けた学生のテストスコア (例: [70, 72, 78, 76])
- グループ C: プログラム C を受けた学生のテストスコア (例: [88, 92, 94, 96])
分析の手順
- 仮説の設定
- 帰無仮説 (H₀): プログラム間にテストスコアの差はない(全グループの中央値は等しい)。
- 対立仮説 (H₁): 少なくとも1つのプログラムが他と異なる影響を与えている。
- Kruskal-Wallis検定を実施
例としてPythonで検定を行います
import scipy.stats as stats
group_A = [75, 80, 85, 90]
group_B = [70, 72, 78, 76]
group_C = [88, 92, 94, 96]
# Kruskal-Wallis検定
stat, p = stats.kruskal(group_A, group_B, group_C)
print(f"検定統計量: {stat}, p値: {p}")
- 結果の解釈
- p値が0.05未満であれば、帰無仮説を棄却し、「プログラム間に有意差がある」と判断します。
- 次に、多重比較検定(Dunn検定など)を行い、どのプログラム間で差があるのかを特定します。
- 結論
例えば、結果が以下のようになったとします:- プログラム A と B の間に差はない。
- プログラム A と C、B と C の間には有意差がある。
この場合、プログラム C が最も効果的だと結論付けられます。
応用例 2: 病院での治療効果比較
背景
3つの異なる治療法(治療A, 治療B, 治療C)の効果を調べるため、患者の回復時間(日数)を比較します。ただし、回復時間の分布が偏っている(正規分布していない)ため、Kruskal-Wallis検定を使用します。
データの設定
- 治療 A: [7, 9, 8, 10, 9]
- 治療 B: [10, 12, 11, 13, 12]
- 治療 C: [6, 5, 7, 6, 5]
手順と解釈
検定結果でp値が0.05未満であれば、帰無仮説を棄却し、治療法間で回復時間に有意な差があると結論付けます。その後、多重比較検定で具体的にどの治療法が他より優れているかを特定します。
応用例 3: マーケティング施策の効果測定
背景
企業が3つの異なる広告キャンペーン(キャンペーンX, Y, Z)を実施しました。それぞれのキャンペーンによるクリック率(CTR)を比較し、どの施策が最も効果的かを判断したいとします。ただし、CTRデータが偏りを持つため、正規分布を仮定できません。
データの設定
- キャンペーン X: [2.5%, 3.0%, 2.8%, 2.7%]
- キャンペーン Y: [1.8%, 2.0%, 1.9%, 1.7%]
- キャンペーン Z: [3.5%, 3.8%, 3.6%, 3.7%]
結果の活用
仮説検定を通じて、キャンペーンZが他のキャンペーンより有意にクリック率を向上させていることが分かれば、次回以降の施策設計において、このキャンペーン手法を採用するなどの戦略が立てられます。
応用例 4: 製品テストでの好感度評価
背景
企業が3つの異なる製品デザイン(デザインA, デザインB, デザインC)を市場テストしました。テスト参加者から集めた評価スコアが正規分布しなかったため、Kruskal-Wallis検定で評価スコアの違いを比較します。
結論
例えば、デザインCが最も高いスコアを得た場合、このデザインを採用することで市場の受容性を高められる可能性があります。
実務でのポイント
- データの確認: 分布やデータタイプ(順序尺度、間隔尺度など)を確認し、Kruskal-Wallis検定が適切かを判断します。
- 多重比較検定の実施: 帰無仮説を棄却した場合、追加分析でどのグループ間に差があるのかを明らかにする必要があります。
- ビジネスインパクトの解釈: 統計的に有意な結果を基に、どのような行動を取るべきかを明確化します。
Kruskal-Wallis検定は、さまざまな分野で実務的な洞察を得るために活用できる強力なツールです。ぜひ、応用例を参考に実務でも試してみてください!
まとめ
Kruskal-Wallis検定は、正規性や等分散性を仮定しない場合に非常に便利な検定方法です。データの性質に応じて適切な検定手法を選択することで、より信頼性の高い結論を導くことができます。
未経験者にも取り組みやすい検定なので、ぜひデータ分析に取り入れてみてください!
統計手法を「知っている」だけでは実務では足りない
ここまで解説してきた統計手法は、
データの差や関係性を判断するうえで非常に重要な道具です。
一方で、実務の現場では
「統計的に有意かどうか」だけで意思決定が行われることはほとんどありません。
たとえば、
・その差は施策として採用する価値があるのか
・他の指標や条件を考慮しても再現性があるのか
・実際の業務データ(欠損・歪み・外れ値)でも同じ結論になるのか
といった観点まで含めて判断されます。
そのため、統計手法そのものに加えて、
データの前処理、可視化、モデル構築、結果の解釈と説明までを
一連の流れとして理解しておくことが重要になります。
統計を「仕事で使う」ために次に必要なこと
検定や分布の考え方を理解したあと、
次に多くの人がつまずくのが
「では、この知識をどうやって実務に落とし込めばいいのか?」
という点です。
実務では、
・PythonやSQLを使ったデータ取得・前処理
・分析結果の可視化と説明
・ビジネス上の意思決定への落とし込み
までを一貫して行う必要があります。
こうした流れを体系的に学ぶ選択肢の一つとして、
データ分析を実務ベースで学べる講座があります。

本サイト で扱っているような統計手法の理解は、
データ分析を行ううえでの重要な基礎になります。
DMM WEBCAMP のデータサイエンスコースでは、
こうした理論的知識を前提として、
実際の業務データを想定した分析フローや実装方法までを体系的に学ぶことができます。
【統計検定 合格に必須の書籍のご紹介】
📘 統計検定2級 おすすめ参考書ランキング【2025年版】
🥇 第1位:統計検定2級公式問題集(最新版)

💴 価格:2,200円(税込)
⭐ 必須レベル:★★★★★
⭐ 難易度:★★★☆☆
⭐ 実践力アップ:★★★★★
✅ 本番と同じ出題形式
✅ 解説が詳細で学習のペースをつかみやすい
✅ 独学でも十分に対応可能
🥈 第2位:統計検定2級対応 統計学基礎

💴 価格:2,420円(税込)
⭐ 必須レベル:★★★★☆
⭐ 難易度:★★★★☆
⭐ 実践力アップ:★★★☆☆
🥉 第3位:統計検定準1級対応 統計学実践ワークブック

💴 価格:3,080円(税込)
⭐ 必須レベル:★★★☆☆
⭐ 難易度:★★★★★
⭐ 実践力アップ:★★★☆☆
📗 統計検定3級 おすすめ参考書ランキング【2025年版】
🥇 第1位:統計検定3級公式問題集(最新版)

💴 価格:2,200円(税込)
⭐ 必須レベル:★★★★★
⭐ 難易度:★★☆☆☆
⭐ 実践力アップ:★★★★☆
✅ 出題形式そのまま
✅ 解説がわかりやすい
✅ 本番前の力試しにも最適
🥈 第2位:やさしくわかる統計学のための数学

💴 価格:2,420円(税込)
⭐ 必須レベル:★★★☆☆
⭐ 難易度:★☆☆☆☆
⭐ 理解のしやすさ:★★★★★
✅ 図やカラーで直感的に理解できる
✅ 基礎から丁寧に解説
✅ 3級の出題範囲を広くカバー
🥉 第3位:マンガでわかる統計学

💴 価格:1,870円(税込)
⭐ 必須レベル:★★☆☆☆
⭐ 難易度:★☆☆☆☆
⭐ 楽しさ・読みやすさ:★★★★★
✅ 読みやすさ抜群で初心者向け
✅ 3級で出題される用語や考え方に対応
✅ 楽しみながら学べる
📕 統計検定4級 おすすめ参考書ランキング【2025年版】
第1位:統計検定4級公式問題集(最新版)

💴 価格:2,200円(税込)
⭐ 必須レベル:★★★★★
⭐ 難易度:★★☆☆☆
⭐ 実践力アップ:★★★★☆
✅ 出題形式そのまま
✅ 解説がわかりやすい
✅ 本番前の力試しにも最適
🥈 第2位:基礎から学ぶ統計学

💴 価格:3,520円(税込)
⭐ 必須レベル:★★★☆☆
⭐ 難易度:★★★★☆
⭐ 楽しさ・読みやすさ:★★☆☆☆
✅ 専門的な用語などを徹底的にわかりやすく表現
✅ 図やキャラの会話で直感的に学べる
🥉 第3位:Excelで学ぶはじめての統計学

💴 価格:2,200円(税込)
⭐ 必須レベル:★★★☆☆
⭐ 難易度:★★☆☆☆
⭐ 実践力アップ:★★★★★
✅ 実践重視の学習に◎
✅ 表計算ソフトの基本操作も習得可能
✅ 講義+演習形式で4級範囲をカバー
📌 参考書選びのポイント(級別)
4級:小〜中学生レベル。グラフ・表・言葉の意味を理解するところから
2級:大学初級〜中級レベル。理論と実践のバランスが必要
3級:高校数学+基礎統計。用語と計算に慣れるのがカギ