1. 最小二乗法とは?
最小二乗法は、与えられたデータセットに対して、回帰直線を引く際に、各データ点と直線との距離(誤差)の二乗和を最小化する方法です。この方法により、最も誤差が少ない直線を導き出すことができます。
2. 最小二乗法の数式
最小二乗法の基本的な考え方は、観測値 yi と予測値 y^i の誤差(残差) ϵi=yi−y^i の二乗和を最小にすることです。残差の二乗和は以下のように表されます。
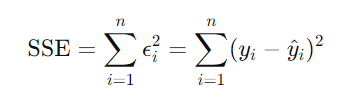
ここで、y^i=a+bxiは予測直線の方程式です。この二乗和を最小にする a と b の値を求めることが、最小二乗法の目的です。
とはいってもなんのために予測直線を使うのかわかりにくいので、実例でお話します。
以前の記事で単回帰分析について解説しました。
単回帰分析についてわかりやすく解説
単回帰分析は『ある1つの説明変数が目的変数にどのような影響を与えるかを定量的に把握するための手法』と解説しましたが、この際考えるのは散らばったデータの間に一番都合よく通る直線を引くことです。
下記の図で解説すると、青色の観測値がありこれらのデータは散らばってプロットされてます。
各観測値の間を一番都合よく通る直線が赤色の直線になります。
そして黒の点線が各観測値から赤色の直線までの距離で、これが残差となります。
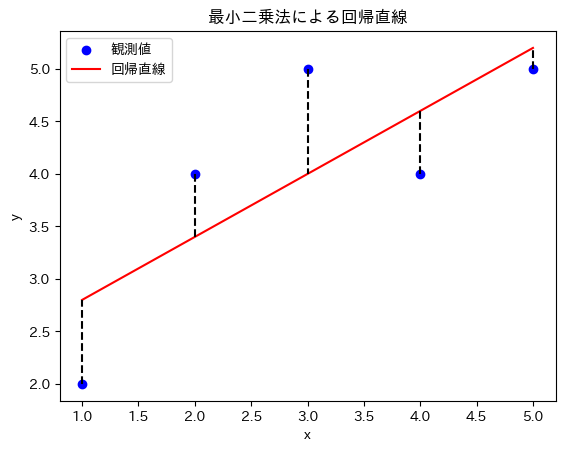
最小二乗法というのは、この黒の点線の距離を最小にする直線はどれか?を明らかにする方法です。
3. 最小二乗法の導出
最小二乗法を用いて、回帰直線の傾き b と切片 a を計算するためには、以下のような公式を使用します。
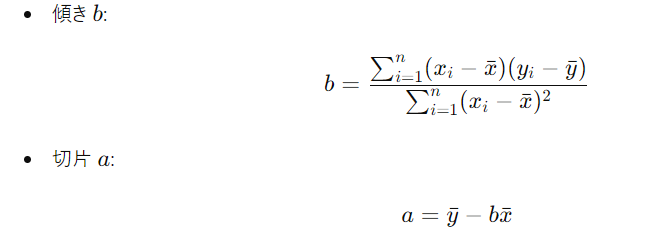
ここで、xˉ と yˉ はそれぞれ x と y の平均値です。
4. 最小二乗法の応用例
最小二乗法は、様々な分野で応用されています。例えば、経済学では需要と供給の関係をモデル化する際に使用され、物理学では実験データに基づいて物理法則を推定する際にも利用されます。
先ほど示した通り、説明変数と目的変数を用いる単回帰分析において最小二乗法を活用することで、最適な直線を求めることが出来ます。
単回帰分析の基礎となる部分となりますのでしっかり理解しておくとよいです。




