統計学では、「どんな確率で特定の事象が起こるか」を分析することが重要です。その中でも多項分布は、複数のカテゴリに分類されるデータを扱うときに役立つ確率分布です。この記事では、多項分布の基本から、実際にどう使われるかをわかりやすく解説します!
多項分布とは?
多項分布は、次のような状況で使われる確率分布です。
- 1回の試行で複数の結果が出る可能性がある(例:サイコロの目)。
- 試行が独立して繰り返される(例:複数回のサイコロ振り)。
- 各結果がそれぞれの確率を持つ(例:サイコロの目が均等に出る場合、各目の確率は 1/6
具体例:サイコロの出目
6面のサイコロを10回振ったとしましょう。出た目(1~6)の個数を知りたい場合、多項分布を用いることで確率を計算できます。
このとき、次の条件が成り立ちます:
- 試行回数:n=10
- 結果のカテゴリ数:6(1~6の目)
- 各カテゴリが出る確率:p1=p2=⋯=p6=1/6
数式で見る多項分布
多項分布は、以下の数式で表されます:
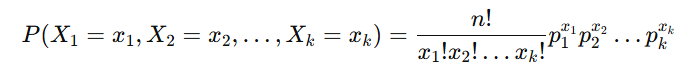
記号の意味
- n:試行回数(例:10回サイコロを振る)
- k:カテゴリ数(例:サイコロの6面)
- xi:カテゴリ i の発生回数(例:1の目が出た回数)
- pi:カテゴリ i が発生する確率(例:サイコロの1が出る確率 1/6)
多項分布の特徴
1. カテゴリの発生回数の合計は一定
多項分布では、すべてのカテゴリの発生回数を合計すると試行回数に一致します:
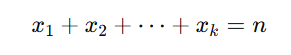
2. 各カテゴリの確率は固定
試行が独立しているため、1回の試行でカテゴリ iii が発生する確率 pi は一定です。
実際の活用例
多項分布は、以下のような場面で応用されています。
1. アンケート分析
例えば、5つの選択肢から1つを選ぶアンケートを100人に実施した場合、各選択肢の回答数が多項分布に従うと仮定して分析できます。
2. 製品の検査
工場で生産される製品が「良品」「欠陥品」「破損品」の3カテゴリに分類される場合、一定数の検査結果から全体の品質状況を推定できます。
Pythonで多項分布をシミュレーション
Pythonを使うと、多項分布のシミュレーションを簡単に実行できます。例えば、サイコロを10回振るシミュレーションをしてみましょう。
import numpy as np
# サイコロを10回振る
n = 10 # 試行回数
p = [1/6] * 6 # 各目の確率
result = np.random.multinomial(n, p)
print("サイコロの出目の回数:", result)
まとめ
多項分布は、複数の結果がある場合にそれぞれの発生確率を扱う便利なツールです。アンケートや製品検査など、日常的なデータ分析にも応用されています。次に確率を扱う際は、多項分布を活用してみてください!
データ分析のキャリアを目指すあなたへ!
統計学や機械学習は、データサイエンスやAIエンジニアリングの基盤となる分野です。
こうした知識を深め、実践的なスキルを身につければ、需要の高いAI関連職種でのキャリア形成も目指せます。
未経験からでも安心して学べるおすすめのキャリア支援サービスについて、こちらの記事で詳しく解説していますので、ぜひチェックしてみてください。