偏相関係数は、統計学やデータ分析において重要な指標の一つで、2つの変数の間の関係を他の変数の影響を取り除いた状態で測定するものです。本記事では、偏相関係数の定義、計算方法、実用例を詳しく解説します。
偏相関係数とは?
偏相関係数(Partial Correlation Coefficient)とは、2つの変数 X と Y の相関を、第三の変数 Z の影響を排除して測定する指標です。
通常の相関係数では、すべての要因を含んだ状態で変数間の関係を測定しますが、偏相関係数を使うことで、特定の要因が関係にどの程度影響を与えているかを評価できます。
偏相関係数の数式
偏相関係数は、以下の数式で計算されます:
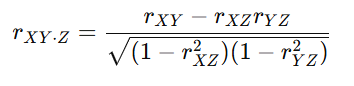
各記号の意味
- rXY:X と Y の通常の相関係数
- rXZ:X と Z の相関係数
- rYZ:Y と Z の相関係数
この式を使うことで、第三の変数 Z の影響を除去した X と Y の純粋な相関を得ることができます。
偏相関係数を使う目的
1. 多変量データの関係性を理解
偏相関係数は、データ内の変数間の独立した関係性を明らかにするために使われます。
例
健康データで、体重 (X) と血圧 (Y) の関係を調べたい場合、運動習慣 (Z) が影響を及ぼす可能性があります。偏相関係数を計算することで、運動習慣を取り除いた体重と血圧の純粋な関係を評価できます。
2. 変数の影響を制御した分析
偏相関係数は、回帰分析や因果関係の解明において重要な役割を果たします。
例
マーケティングデータで、広告費用 (X) と売上 (Y) の関係を調べる際に、季節要因 (Z) を取り除きたい場合に利用します。
偏相関係数の計算手順
以下は、具体的な例を使った計算手順です。
例題
データセットには以下の3つの変数が含まれています:
- X:勉強時間
- Y:試験の点数
- Z:睡眠時間
3変数間の相関係数が以下のように与えられています:
- rXY=0.8
- rXz=0.6
- ryz=0.5
偏相関係数 rXY⋅zを計算します。
ステップ1:公式に代入
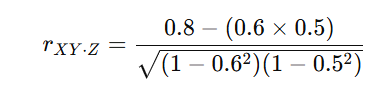
ステップ2:計算
分子:
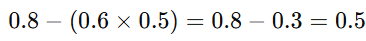
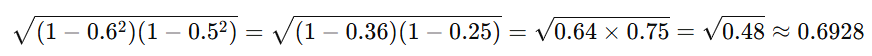
結果:
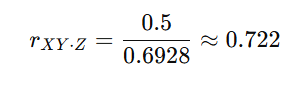
この場合、偏相関係数は約 0.72 です。
実用例
医療分野
患者の健康状態を分析する際に、偏相関係数を用いて特定の要因(例:年齢や性別)が他の因子間の関係にどの程度影響しているかを調べます。
具体例
- X:食事の栄養バランス
- Y:血圧の安定度
- Z:運動頻度
ビジネス・マーケティング
消費者行動データを分析する際、季節要因や経済状況などの影響を除外して、広告効果の実質的な影響を評価します。
具体例
- X:広告費用
- Y:売上
- Z:経済成長率
偏相関係数の限界
- 因果関係は明らかにできない
偏相関係数は相関を測定する指標であり、因果関係を示すものではありません。 - 多重共線性の影響を受ける
変数間に強い相関がある場合、計算結果が不安定になることがあります。 - 非線形関係は測定できない
偏相関係数は線形関係を前提としており、非線形な関係を正確に測定することはできません。
まとめ
偏相関係数は、特定の要因を制御した状態で変数間の関係を測定する便利な統計指標です。特に、データの複雑な関係性を明らかにしたい場合に役立ちます。ただし、その限界を理解した上で、他の統計手法と組み合わせて活用することが重要です。
偏相関係数をマスターすることで、データ分析の精度をさらに高めることができるでしょう!