目次
1. ポアソン分布とは？
ポアソン分布は、一定の時間や空間において、稀なイベントが発生する回数をモデル化するための確率分布です。この分布は、フランスの数学者シメオン・ドニ・ポアソンによって導入されました。ポアソン分布は、特にイベントが独立して発生し、その発生率が一定である状況に適用されます。
実例1: レストランの注文
あるレストランでは、1時間に平均して5人の客が注文をします。しかし、客が来るタイミングは不規則で、全く来ない時もあれば、短い間に何人も来ることもあります。このような状況では、1時間に何人の客が来るかをポアソン分布で予測できます。たとえば、「1時間に10人以上の客が来る確率はどれくらいか？」を計算することができます。
実例2: 救急車の出動回数
ある地域で、救急車が1日に呼び出される平均回数が2回だとします。しかし、呼び出しがいつ発生するかは予測できません。このような場合に、1日に救急車が何回呼び出されるかをポアソン分布を使って予測できます。たとえば、「1日に4回以上呼び出される確率はどれくらいか？」といった質問に答えることができます。
ポアソン分布は、このような「ある時間や空間での稀な出来事がどれくらいの頻度で発生するか」をモデル化するために非常に有用です。特に、イベントが独立して発生し、その発生率が一定である場合に適用されます。
2. ポアソン分布の定義と式
ポアソン分布は次のように定義されます。
- 確率質量関数 (PMF): ポアソン分布に従うランダム変数 X が、平均発生率 λ に基づいて k 回のイベントを観測する確率は以下の式で表されます。
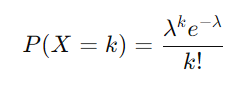
ここで、
- λ は一定の時間や空間における平均発生率（正の実数）。
- k は観測されるイベントの回数（非負の整数）。
- e はネイピア数（自然対数の底）。
3.ポアソン分布と期待値
ポアソン分布における期待値（平均）は非常に重要な要素です。ポアソン分布の特徴として、期待値と分散が同じ値を持つという性質があります。この期待値は、分布全体の中心を示し、平均的にどれくらいのイベントが発生するかを表します。
ポアソン分布において、ランダム変数 X が発生する回数を表し、その平均発生率を λ とすると、期待値 E(X) は次のように定義されます。
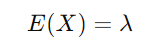
この式からわかるように、λ はポアソン分布における平均発生回数を直接表します。したがって、λ が大きいほど、観測されるイベントの回数は多くなり、小さいほど少なくなります。
期待値と分布の形状
ポアソン分布の期待値 λ に応じて、分布の形状も変化します。
- λ が小さい場合: 分布は0に近い値に集中し、イベントがほとんど発生しないことを示します。
- λ が大きい場合: 分布はより広がり、イベントが頻繁に発生することを示します。この場合、分布は正規分布に近づく傾向があります。
期待値の解釈と応用
期待値は、実務上でポアソン分布を利用する際の基本的な指標です。例えば、以下のような応用があります。
- 医療: 病院で1日に発生する患者の数の期待値を求めることで、必要な医療リソースを効率的に配置することができます。
- マーケティング: ウェブサイトへの1日のアクセス数の期待値を基に、サーバーの負荷を予測し、必要なインフラを準備することができます。
- 製造業: 生産ラインで発生する欠陥品の期待値を計算し、品質改善の目標設定に利用できます。
ポアソン分布の期待値は、分布全体を理解するための基本的な概念であり、現実の問題に適用する際の出発点となります。これにより、どのような状況でどの程度の頻度でイベントが発生するかを予測し、適切な対応策を講じることができます。
4. ポアソン分布の特徴
- 期待値と分散が等しい: ポアソン分布の期待値（平均）と分散はともに λ\lambdaλ です。
- 離散的な確率分布: ポアソン分布は、整数値（0, 1, 2, …）をとる離散確率分布です。
- 稀なイベント: ポアソン分布は、特に「稀なイベント」を扱う際に有効です。たとえば、特定の時間内に電話がかかってくる回数や、一定の区域内で起こる交通事故の回数などがこれに該当します。
5. ポアソン分布の使用例
- 電話交換の呼び出し: 通信ネットワークにおける通話の到着数のモデル化。
- 交通事故の発生: 特定の交差点で一定期間に発生する交通事故の数。
- ウェブサイトへのアクセス: 一定時間内に特定のウェブページにアクセスされる回数。
6. ポアソン分布の導出 ～二項分布との関連性～
ポアソン分布は、二項分布の特殊な場合として導出されます。具体的には、次の条件を満たすときにポアソン分布が現れます。
- 試行回数 n が非常に大きい（n→∞）
- 個々の試行で成功する確率 p が非常に小さい（p→0）
- 試行回数 n と成功確率 p の積 np が一定の値に近づく
この一定の値 np を λ とすると、二項分布はポアソン分布に収束します。
導出の数学的背景
二項分布の確率質量関数（PMF）は以下のように表されます。
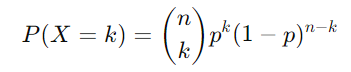
ここで、nnn が非常に大きく、ppp が非常に小さい場合、次の近似が成り立ちます。
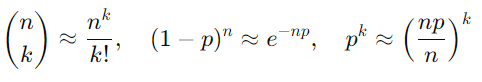
これらを二項分布の式に代入すると、ポアソン分布の式に近似されます。
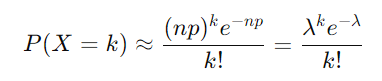
この結果、ポアソン分布は、稀に発生するイベントの回数をモデル化する場合に適した分布となります。
7. ポアソン分布の関連分布
ポアソン分布は、他のいくつかの確率分布と密接に関連しています。特に、ポアソン過程という概念を通じて理解すると、これらの関連性がより明確になります。
(1) 指数分布
ポアソン過程では、イベントが連続的に発生する時間間隔が重要です。この時間間隔は、指数分布に従います。具体的には、イベントが発生するまでの待ち時間が指数分布に従い、ポアソン分布はその発生回数をモデル化します。
- 例: レストランで次の客が注文をするまでの時間が指数分布に従うと仮定することで、その時間の間に何人の客が来るかをポアソン分布でモデル化できます。
(2) ガンマ分布
ポアソン分布の累積的な結果がガンマ分布に関連します。具体的には、複数の独立したポアソン分布が合わさるとガンマ分布を形成します。
- 例: 複数のレストランが独立して存在し、それぞれで1時間に何人の客が来るかがポアソン分布に従う場合、すべてのレストランの合計で何人の客が来るかはガンマ分布で表されます。
(3) 正規分布
ポアソン分布の平均 λ\lambdaλ が大きくなると、中心極限定理により、ポアソン分布は正規分布に近似されます。このため、大規模なサンプルでは、ポアソン分布を正規分布で近似することが可能です。
- 例: 非常に多くの注文が発生する大規模なレストランチェーンでは、1日に受ける総注文数が正規分布に近似されます。
8. 実務での応用
ポアソン分布は、マーケティングや医療、工学、保険など、多くの分野で応用されています。特に、頻度分析やリスク評価、データの予測モデルなどで利用されています。
(1) マーケティング
ポアソン分布は、マーケティングキャンペーンの効果を評価する際に利用されます。たとえば、ある製品のウェブサイトに1日にアクセスするユーザーの数がポアソン分布に従うと仮定することで、キャンペーンによってアクセス数がどれほど増加するかを予測できます。
- 具体例: 特定の商品ページへの1日のアクセス数をモデル化し、広告キャンペーンの前後でアクセス数の変化を分析します。
(2) 医療分野
ポアソン分布は、特定の期間に発生する病気の症例数や、病院での緊急手術の回数などをモデル化するのに使用されます。
- 具体例: 病院が1日に対応する緊急手術の数をモデル化し、必要な医療リソースの配置を計画します。
(3) 工学
製造プロセスで発生する欠陥品の数を予測するためにポアソン分布が使われます。これにより、品質管理や製品の信頼性を評価することができます。
- 具体例: 生産ラインで1時間に発生する欠陥品の数をポアソン分布でモデル化し、製造品質の評価を行います。
(4) 保険業
保険会社は、ポアソン分布を使用して、特定の期間に発生する保険請求の数を予測し、リスクを評価します。
- 具体例: 自動車保険で、特定の期間に発生する事故件数をポアソン分布でモデル化し、保険料の設定に利用します。
9. ポアソン分布の限界と注意点
ポアソン分布を適用する際には、イベントが独立していること、そして発生率が一定であることが前提となります。この条件が満たされない場合には、ポアソン分布は適切でない可能性があります。
10. まとめ
ポアソン分布は、ランダムに発生する稀なイベントの数をモデル化するための強力なツールです。その特徴や応用範囲を理解することで、さまざまな実務上の問題に対応できるようになります。
データサイエンスの資格取得したい方へ おすすめの資格
データサイエンス資格一覧 – 資格の種類やそのメリットを紹介
