はじめに
統計学や機械学習の分野では、ベイズの定理が非常に重要な役割を果たしています。ベイズの定理は、既存の情報に新たなデータを組み合わせることで、確率を更新していく方法を提供します。この記事では、ベイズの定理の基本的な考え方から、Pythonを用いた実際の実装例までをわかりやすく説明します。
1. ベイズの定理とは?
ベイズの定理は、事象の確率を「既に知っていること」と「新たに得た情報」に基づいて更新するための数式です。具体的には、以下のように表されます。
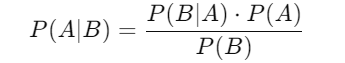
記号の意味
- P(A∣B):事後確率。新しい情報 BBB に基づいて、事象 AAA が発生する確率です。
- P(B∣A):尤度。事象 AAA が発生した場合に、情報 BBB が得られる確率です。
- P(A):事前確率。事象 AAA が発生する前の既存の確率です。
- P(B):周辺確率。情報 BBB が得られる全体の確率です。
2. ベイズの定理の具体例
実際の生活でベイズの定理がどのように使われるかをイメージしてみましょう。たとえば、医療検査を考えます。
医療検査の例
ある病気にかかっている確率(事前確率)は 1% だとします。また、その病気の検査で陽性となる確率(感度)は 90%、一方で実際には病気でないのに検査が陽性になる確率(偽陽性率)は 5% です。このとき、検査が陽性となった場合に実際に病気である確率を計算することができます。
このようなシナリオは、ベイズの定理を使うことで、より正確に病気にかかっている確率を求めることが可能です。
3. ベイズの定理の応用
ベイズの定理は、多くの分野で応用されています。ここでは、いくつかの代表的な応用例を紹介します。
機械学習における応用
- ナイーブベイズ分類器:機械学習において、ベイズの定理を基にした分類アルゴリズムで、スパムメールの分類やテキスト分類などに利用されています。
- ベイズ最適化:機械学習モデルのハイパーパラメータの最適化に用いられる手法です。
デジタルマーケティングでの応用
- 広告のクリック予測や顧客行動の予測において、ベイズの定理を使って新しいデータが得られるたびにモデルを更新することができます。
4. Pythonでベイズの定理を実装してみよう
ベイズの定理の理解を深めるために、実際にPythonを使って簡単な実装を行ってみましょう。ここでは、先ほどの医療検査の例を使って、陽性反応が出たときの病気である確率を計算します。
# 事前確率 P(A) = 0.01(病気の確率)
P_A = 0.01
# 感度 P(B|A) = 0.9(病気のとき陽性となる確率)
P_B_given_A = 0.9
# 偽陽性率 P(B|¬A) = 0.05(病気でないのに陽性となる確率)
P_B_given_not_A = 0.05
# 事前確率 P(¬A) = 1 - P(A)(病気でない確率)
P_not_A = 1 - P_A
# 周辺確率 P(B) = P(B|A) * P(A) + P(B|¬A) * P(¬A) (全体の陽性率)
P_B = (P_B_given_A * P_A) + (P_B_given_not_A * P_not_A)
# ベイズの定理による事後確率 P(A|B) = (P(B|A) * P(A)) / P(B)
P_A_given_B = (P_B_given_A * P_A) / P_B
# 結果を出力
print(f"検査が陽性だった場合の実際の病気である確率 P(A|B) は: {P_A_given_B:.4f}")
実行結果
検査が陽性だった場合の実際の病気である確率 P(A|B) は: 0.1538
この結果からわかるように、検査が陽性であっても、実際に病気である確率は約 15.38% です。これは、事前確率が低い場合には、検査の結果が陽性であっても実際の病気の確率が必ずしも高くないことを示しています。
5. まとめ
ベイズの定理は、情報が新たに得られるたびに確率を更新できる強力なツールです。この記事では、ベイズの定理の基本的な公式から、医療検査の例を用いて実際にどのように計算するのかを解説しました。また、Pythonでの実装例を通じて、実際の問題にどのように適用できるかも紹介しました。
ベイズの定理は、機械学習やデジタルマーケティングの分野だけでなく、幅広い分野で応用されています。ぜひ、この概念を理解して、データに基づいた意思決定に活用してみてください。



