今回は統計検定2級の範囲である単回帰分析についてわかりやすく解説します。
単回帰解析は『知りたい変数がどれぐらい別の変数によって説明できるのか?』という問いに答えてくれます。
本記事では、解析の手法から例題までを解説しています。
単回帰分析の目的
例えば収入と学歴の関係について考えます。
『学歴は収入に関係するのか?』ということを明らかにしたい場合ですね。
それぞれ収入を調査の対象とする変数(目的変数)と学歴を目的変数を説明できそうな要因っぽい指標の変数(説明変数)と呼びます。
ここで大事なのは、説明変数として置くのはあくまで『要因っぽい指標』と思うことで、後述の計算でも出てきますが、必ずしも関係するわけではない or 関係して当たり前の要因ということです。ここはざっくりと頭に入れておくといいのかなと思います。
なので、単回帰分析の目的としては、解き明かしたい目的の変数を1つの指標(単回帰)としてどれだけ説明できるのか?ということです。
単回帰分析の手順
単回帰分析とは、ある1つの説明変数が目的変数にどのような影響を与えるかを定量的に把握するための手法です。ここでは、学歴(説明変数)が年収(目的変数)に与える影響を調べます。
例えば、以下のような回帰モデルを考えます。
年収=β0+β1×学歴+ϵ
この式の意味は、年収は学歴の関数として表され、β0が切片、β1が学歴による年収の変化率を示す回帰係数です。ここで、ϵは誤差項で、学歴以外の要因からの影響を表します。
で、学歴は数字で表せないので、学校に通った年数にしましょう。
「学歴が高いほど年収が高い」と言われることが多いですが、実際にどの程度の関係があるのでしょうか?今回は、年収を目的変数に、学歴を説明変数にした単回帰分析を通じて、その関係性を具体的なデータで探ります。
Step1.β0、β1の数値を取得
β0、β1の数値を取得しましょう。
多くの場合、下記のように表として既に計算されているものがあるので、
この表から読み解いていきます。
| 学歴(年) | 年収(万円) |
| 12 | 300 |
| 16 | 500 |
| 18 | 600 |
| 20 | 700 |
| 22 | 800 |
この表では、学歴が12年(高校卒業程度)の人は年収300万円、学歴が22年(大学院卒業程度)の人は年収800万円としています。
まず、回帰係数 β1 を求めます。
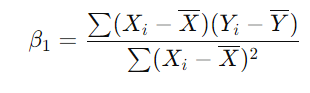
ここで、X̄は学歴の平均、Ȳは年収の平均です。
平均値を計算すると
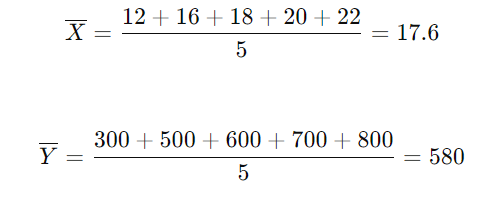
となります。
こちらを
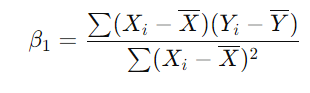
に代入すると、
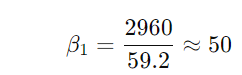
という値が得られます。こちらでβ1が求められたので、先ほどの回帰式にXとYの平均値とβ1を代入すると
β0=Y−β1×X
β0=580−50×17.6=580−880=-300
となります。
以上をもって、β0=-300 β1=50となり、以下のような回帰式が得られました。
年収=-300+50×学歴
この式によると、学歴が1年増えるごとに年収は50万円増えることが示されています。
例えば、学歴が16年(大学卒業)の場合、年収は以下のように計算されます。
年収=-300+50×16=500万円
Step2.結果を解釈する
この結果から、「学歴が高くなるほど年収が高くなる」という一般的な傾向が確認されました。
ただし、これはあくまで学歴に基づく年収の一部を説明するモデルであり、全ての要因を考慮したものではありません。実際には、経験、業種、地域など、多くの要因が年収に影響を与えます。
単回帰分析を通じて、学歴と年収の関係を定量的に示すことができました。学歴は確かに年収に影響を与える一つの要因ですが、それが全てではないことを忘れてはなりません。年収を上げるためには、学歴だけでなく、多様なスキルや経験の積み重ねが重要です。
データを活用して現実の問題を理解する方法として、単回帰分析は非常に有用です。今後も多くの要因を取り入れた複雑なモデルを用いて、より深い洞察を得ることが期待されます。