はじめに
生存分析は医学、工学、経済学など多岐にわたる分野で用いられる強力な統計手法です。この記事では、特に「生存関数」と呼ばれる重要な概念に焦点を当て、その基本と応用について解説します。
生存関数とは？
生存関数、または生存確率関数は、統計学において特定の時間までにイベント（例えば、機械の故障や患者の死亡）が発生しない確率を表します。
この関数は、時間とともにどのように確率が変化するかを示し、生存分析の基本的なツールとなります。
生存関数の計算方法
生存関数 S(t)は、通常
S(t)=1−F(t)
で表されます。
ここで F(t) は累積分布関数で、時間 t までにイベントが発生する確率を示します。
また、生存関数は
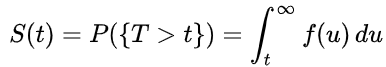
としても表されることがあり、ここで T は生存時間の確率変数、t>0 は生存時間の実現値、f は生存時間の確率密度関数を表します。
実例での計算
例として、ある新薬が患者の生存期間に与える影響を分析する場合を考えます。
治療群と対照群での生存関数をプロットし、これらの生存曲線を比較することで新薬の効果を評価します。具体的には、各群の患者のフォローアップデータから生存関数を推定し、グラフにして視覚的に比較します。このような分析により、新薬の治療効果が統計的に有意であるかどうかを判断することができます。
生存関数の実際の計算例を示します。
がん治療の効果を評価するために、患者の生存データを分析する場面を想定します。100人の患者が新しい治療法を受け、フォローアップ期間中に30人が死亡しました。時間 t はフォローアップの期間（例えば月単位）です。
生存関数 S(t) を計算するために、各時間点での生存確率を積み重ねて全体の生存関数を推定します。
具体的な計算ステップは以下の通りです：
- 時間を昇順に並べ、各時間点での死亡数と生存数を記録します。
- 各時間点での生存確率を 生存している患者数−死亡数生存している患者数\frac{生存している患者数 – 死亡数}{生存している患者数}生存している患者数生存している患者数−死亡数 で計算します。
- 各時間点での生存確率を前の時間点までの生存確率と乗算し、累積生存確率を求めます。
この計算を続けて、最終的な生存曲線を描きます。この方法により、治療効果や他の危険因子の影響を統計的に分析することが可能です。
結論
生存関数は、生存時間データの解析において中心的な役割を担います。この関数を理解し活用することで、より正確な予測と効果的な意思決定が可能になります。生存分析の基本をマスターすることで、あなたの分析スキルは大きく向上するでしょう。
参考書や転職サイトの紹介
z検定やt検定をはじめとする統計学の知識は、データ分析やビジネスにおいてますます重要性が高まっています。これらの知識を深めるために役立つ参考書や、キャリアアップを目指す方におすすめの転職サイトをいくつかご紹介します。
統計学の参考書
『統計学が最強の学問である』西内啓 著
『統計学が最強の学問である』は、統計学が現代社会でいかに強力なツールであるかを解説した一冊です。
データを扱う際に不可欠な考え方を実例とともに学べるため、ビジネスや日常生活に統計学を応用したい人にとって理想的な入門書です。特に、難解な数式を避け、具体的な事例や比喩を用いて説明するため、初学者でも「統計学の力」を体感できる内容になっています。
『世界一やさしい統計学の教科書 1年生』
文系の方が統計学に取り組む際に直面するハードルを意識し、難しい数式や理論を極力排除しながら、統計学の基本概念を丁寧に解説しています。
さらに、各章ごとに理解度を確認するための演習問題が用意されており、自分のペースで着実に学びを深めることができます。
データサイエンティストへの転職サポート/資格取得
テックゲート転職
- 特徴
- 未経験者歓迎: ITの基礎から学べる研修などが用意されており、未経験者でもスタートが可能
- 30代転職実績: 年齢を重ねても転職が成功しており、30代の転職実績が豊富にあり
- 転職支援実績: 5000名を超える転職者がこのサービスを利用して新しいキャリアをスタート
- 転職定着率97%: 転職後の定着率が97%と非常に高く、長期的なキャリア形成
オンスク.JP
- 特徴
- 独学での勉強: 様々な資格に関する内容が用意されており、独学でも資格取得が可能
- 月額1,000円台で始められる: 費用の心配も少なくスタートすることが出来ます
- 毎日コツコツ: 1動画5分から視聴でき、ちょっとしたスキマ時間での学習に最適！
統計学の知識を深めつつ、キャリアの新たなステージに進みたい方は、これらの参考書や転職サイトをぜひ活用してください。
