1. はじめに
統計学でよく耳にする「一様分布」。これは確率分布の一種で、特定の範囲内で全ての値が等しい確率で発生することを意味します。
本記事では、一様分布の基本的な概念、特徴、そして実際の応用例について解説します。
2.一様分布の基本
一様分布(Uniform Distribution)は、連続型と離散型に分けられます。連続型の一様分布は、例えば0から1の間のすべての値が等しい確率で選ばれる場合を指します。これを数式で表すと、以下のようになります。
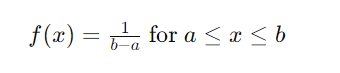
ここで、a と b は分布の範囲を示します。一様分布のグラフは、横軸に値x、縦軸に確率密度f(x)を取ったとき、範囲内で一定の高さを持つ長方形の形をしています。
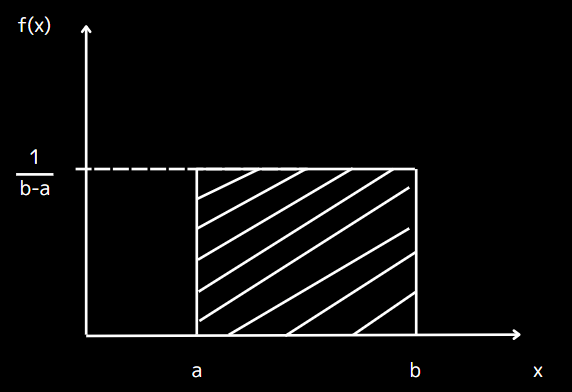
離散型の一様分布
離散型の一様分布は、例えばサイコロを振った時の出目が等しい確率で出る場合を想像すると分かりやすいです。サイコロの場合、各面の出る確率は 1/6 となります。
3.一様分布の特徴
- 平均: 一様分布の平均は、範囲の中央に位置します。これは、
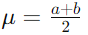
で計算できます。
- 分散: 一様分布の分散は、
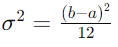
で求められます。
- モード: 一様分布は、範囲内の全ての値が等しい確率で発生するため、特定のモード(最頻値)は存在しません。
4.実際の応用例
一様分布は、ランダムなサンプルを生成したり、モンテカルロシミュレーションなどで広く利用されます。例えば、乱数生成器のアルゴリズムの中では、一様分布が基本的な役割を果たします。また、確率が等しい場合のシミュレーションやモデリングにおいても重要な役割を果たします。
a. 乱数生成
概要: 一様分布は乱数生成アルゴリズムの基礎として広く利用されています。乱数生成器は、一様に分布する数を生成することで、シミュレーションやモンテカルロ法などの様々な統計的手法においてランダム性を確保します。
応用例:
- コンピュータシミュレーション: 乱数を用いて確率過程をシミュレートする際に、一様分布から乱数を生成し、他の分布(例えば正規分布)に変換する手法が取られます。
- 暗号化: 暗号アルゴリズムでは、一様分布から生成される乱数がセキュリティの基盤となります。予測不可能な乱数を生成することが重要です。
b. サンプリング手法
概要: 一様分布は、母集団から無作為にサンプルを選ぶ際に使用されます。例えば、データ分析や調査で母集団全体から等しい確率でサンプルを抽出する場合に一様分布を用います。
応用例:
- 統計調査: 一様分布を利用して、特定の地域や層から無作為にサンプルを抽出し、調査結果を全体に外挿する。
- 機械学習: データセットの分割やクロスバリデーションで、データが偏らないようにするために一様分布を使ってサンプルを選ぶ。
c. モンテカルロ法
概要: モンテカルロ法は、確率的な問題を数値的に解く手法であり、シミュレーションに広く用いられています。一様分布から生成される乱数を利用して、複雑な確率分布や積分の近似を行います。
応用例:
- 金融リスク評価: 株価のシミュレーションやオプション価格の評価において、モンテカルロ法が活用されます。一様分布から乱数を生成し、シナリオ分析を行うことで、リスクの分布を推定します。
- 物理シミュレーション: 粒子の運動や熱拡散など、物理現象をシミュレートする際に、モンテカルロ法を利用してランダムなサンプルを生成します。
d. ランダム試験やゲーム
概要: 一様分布は、ランダム性が求められる試験やゲームにおいて使用されます。公平性を確保するために、全ての結果が等しい確率で起こるように設計されています。
応用例:
- 試験問題のシャッフル: 試験問題をランダムに並び替える際に、一様分布を使用して順序を決定し、公平な試験を実現します。
- カジノゲーム: ルーレットやスロットマシンなど、カジノゲームの結果は一様分布に基づくことが多く、公平なゲームを設計するために活用されます。
e. 生物統計学におけるモデル
概要: 生物統計学では、ある範囲内での現象(例えば動物の移動パターンや細胞分裂のタイミングなど)が一様分布に従うと仮定してモデル化されることがあります。
応用例:
- 生態学: 動物の移動パターンや生息地の選択が一様分布に基づいていると仮定し、保護区の設計や生息数の予測に使用されます。
- 遺伝学: 遺伝子の組み合わせや突然変異の発生頻度が一様分布に基づくと考えられる場合、そのモデルを用いて進化のシミュレーションが行われます。
まとめ
一様分布は、統計学において非常に基本的でありながらも、広範な応用を持つ重要な概念です。統計的な分析やシミュレーションを行う際に、一様分布の理解は欠かせません。特に、ランダム性や確率の公平性を扱う場合において、その利用価値が高まります。




